- We continue to exploit the useful properties of polynomials to develop methods for a computer to do integrations and to find derivatives.
- When the function is explicitly known, we can emulate the methods of calculus. But doing so in getting derivatives requires the subtraction of quantities that are nearly equal and that runs into round-off error.
- However, integration involves only addition, so round-off is not problem; of course, we cannot often find the true answer numerically because the analytical value is the limit of the sum of an infinite number of terms.
- We must be satisfied with approximations for both derivatives and integrals but, for most applications, the numerical answer is adequate.
- If we are working with experimental data that are displayed in a table of [
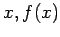 ] pairs emulation of calculus is impossible; we must approximate the function behind the data in some way.
] pairs emulation of calculus is impossible; we must approximate the function behind the data in some way.
- Differentiation with a Computer: Employs the interpolating polynomials to derive formulas for getting derivatives. These can be applied to functions known explicitly as well as those whose values are found in a table.
- Numerical Integration-The Trapezoidal Rule: Approximates, the integrand function with a linear interpolating polynomial to derive a very simple but important formula for numerically integrating functions between given limits.
Subsections
2004-12-21