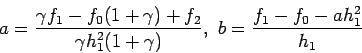- Most of the root-finding methods that we have considered so far have approximated the function in the neighborhood of the root by a straight line.
- Muller's method is based on approximating the function in the neighborhood of the root by a quadratic
polynomial.
- A second-degree polynomial is made to fit three points near a root, at
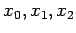 with
with 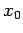 between
between 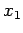 , and
, and 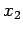 .
.
- The proper zero of this quadratic, using the quadratic formula, is used as the improved estimate of the root.
- A quadratic equation that fits through three points in the vicinity of a root, in the form
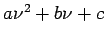 . (See Fig. 1)
. (See Fig. 1)
Figure 1:
Parabola
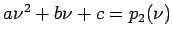
|
|
- Transform axes to pass through the middle point, by letting
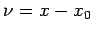 . Let
. Let 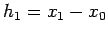 and
and 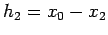 . We evaluate the coefficients by evaluating
. We evaluate the coefficients by evaluating 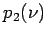 at the three points:
at the three points:
- From the first equation,
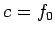 . Letting
. Letting
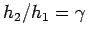 , we can solve the other two equations for a, and b.
, we can solve the other two equations for a, and b.
After computing a, b, and c, we solve for the root of
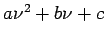 by the quadratic formula
by the quadratic formula
An algorithm for Muller's method :

- Muller's method, like Newton's, will find a complex root if given complex starting values.
Of course, the computations must use complex arithmetic.
- Experience shows that Muller's method converges at a rate that is similar to that for Newton's method. It does not require the evaluation of derivatives, however, and (after we have obtained the starting values) needs only one function evaluation per iteration.
- See Fig. 2 that an example is given
Figure 2:
An example of the use of Muller's method.
|
|
2004-10-18