Matrices and Vectors
- When a system of equations has more than two or three equations, it is difficult to discuss them without using matrices and vectors.
- A matrix is a rectangular array of numbers in which not only the value of the number is important but also its position in the array.
- Two matrices of the same size may be added or subtracted. The sum of
is the matrix whose elements are the sum of the corresponding elements of A and B.
- Similarly, we get the difference of two equal-sized matrices by subtracting corresponding elements. If two matrices are not equal in size, they cannot be added or subtracted.
- Multiplication of two matrices is defined as follows, when A is
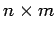 and B is
and B is 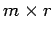 .
.
- Unless the number of columns of A equals the number of rows of B, the matrices cannot be multiplied.
- If A is
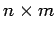 , B must have is
, B must have is 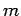 rows or else they are said to be nonconformable for multiplication and
their product is undefined.
rows or else they are said to be nonconformable for multiplication and
their product is undefined.
- In general,
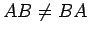 , so the order of factors must be preserved in matrix multiplication.
, so the order of factors must be preserved in matrix multiplication.
- A matrix with only one column,
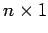 in size, is termed a column vector, and one of only one row,
in size, is termed a column vector, and one of only one row, 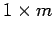 in size, is called a row vector. When the term vector is used, it nearly always means a column vector.
in size, is called a row vector. When the term vector is used, it nearly always means a column vector.
- An
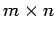 matrix times as
matrix times as 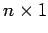 vector gives an
vector gives an 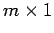 product. The general relation for
product. The general relation for 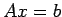 is
is
This definition of matrix multiplication permits us to write the set of linear equations
much more simply in matrix notation, as 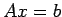 where
where
For example,
is the same as the set of equations
- A vector whose length is one is called a unit vector (The length of a vector is the square root of the sum of the squares of its components, an extension of the idea of the length of a two-component vector drawn from the origin).
- A vector that has all of its elements equal to zero is the zero vector. If all elements are zero except one, it is a unit basis vector. There are three distinct unit basis vectors of order-3:
Subsections
2004-11-03
![\begin{displaymath}
A=\left[
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{...
...y} \right]=\left[a_{ij}\right], i=1,2,\ldots,n, j=1,2,\ldots,m
\end{displaymath}](img1.png)
![\begin{displaymath}
\left[
\begin{array}{ccc}
(a_{11}b_{11}+a_{12}b_{21}+ \ldo...
... (a_{n1}b_{1r}+ \ldots +a_{nm}b_{mr})\\
\end{array} \right]
\end{displaymath}](img7.png)
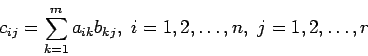
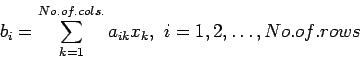
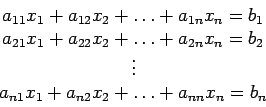
![\begin{displaymath}
A=\left[
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{...
...ay}{c}
b_1\\
b_2\\
\vdots \\
b_n\\
\end{array}\right]
\end{displaymath}](img18.png)
![\begin{displaymath}
\left[
\begin{array}{rrr}
3 & 2 & 4 \\
1 & -2 & 0 \\
-1...
...left[
\begin{array}{r}
14\\
-7\\
2\\
\end{array}\right]
\end{displaymath}](img19.png)
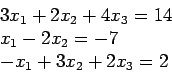
![\begin{displaymath}
\left[
\begin{array}{c}
1\\
0\\
0\\
\end{array}\right...
... \left[
\begin{array}{c}
0\\
0\\
1\\
\end{array}\right]
\end{displaymath}](img21.png)