Ceng 375 Numerical Computations
Final
Jan 19, 2006 13.00-15.00
Good Luck!
1 (25 Pts)
This nonlinear equation is solved by using three methods, namely Bisection, Newton's, Muller's methods. Then, the following tables are obtained.
| iteration |
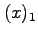 |
 |
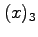 |
| 1 |
0.50000000000000 |
0.33333333333333 |
0.50000000000000 |
| 2 |
0.25000000000000 |
0.36017071357763 |
0.35491389049015 |
| 3 |
0.37500000000000 |
0.36042168047602 |
0.36046467792776 |
| 4 |
0.31250000000000 |
0.36042170296032 |
0.36042169766326 |
| 5 |
0.34375000000000 |
0.36042170296032 |
0.36042170296032 |
| iteration |
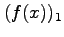 |
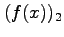 |
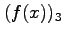 |
| 1 |
3.3070e-01 |
-1.0000e+00 |
3.3070e-01 |
| 2 |
-2.8662e-01 |
-6.8418e-02 |
-1.3807e-02 |
| 3 |
3.6281e-02 |
-6.2799e-04 |
1.0751e-04 |
| 4 |
-1.2190e-01 |
-5.6252e-08 |
-1.3252e-08 |
| 5 |
-4.1956e-02 |
-6.6613e-16 |
2.2204e-16 |
- i
- If the exact value is given as
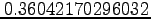 , fill the following tables (use scientific notation as %12.4e, see the table above);
, fill the following tables (use scientific notation as %12.4e, see the table above);
- ii
- Analyze the obtained tables. Is the convergence sustained for the each methods? For the sustained ones; at which iteration and why?
- iii
- What can you say about the speed of convergences for each method?
- iv
- By using your answers for the previous items, fill the following table. You should explain your decision.
- v
- Which method is the best one? Why?
2 (25 Pts) Answer the following questions, choose only 5 of them.
- vi
- Describe the truncation error and round-off error. Give example.
- vii
- What is the ill-conditioned system?
- viii
- What information can be obtained from the determinant of a matrix?
- ix
- Compare the Gaussian elimination and Gauss-Jordan methods, briefly.
- x
- Why do we need pivoting (partial pivoting) while solving sets of equations by elimination methods? Can we skip pivoting and under which circumstances?
- xi
- What does singularity mean for a matrix? Make a comparison of singular and nonsingular matrices.
- xii
- What information can be obtained from the condition number of a matrix?
- xiii
- What are the differences between the interpolation and curve fitting?
3 (20 Pts) For the given data points;
- Write out the Lagrangian polynomial from this table
- xiv
- confirm that it reproduces the
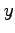 's for each
's for each 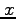 -value.
-value.
- xv
- interpolate with it to estimate
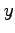 at
at 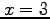 .
.
- xvi
- extrapolate with it to estimate
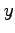 at
at 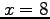 .
.
- Suppose in previous item that the
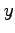 -value for
-value for 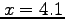 is mistakenly entered as
is mistakenly entered as 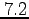 rather than
rather than 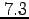 . Repeat the previous item with this incorrect value. How much difference does this make?
. Repeat the previous item with this incorrect value. How much difference does this make?
- Expand the Lagrangian polynomials in the previous items to get the quadratics in the form
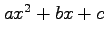 . How different are the values for
. How different are the values for 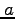 ,
,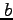 , and
, and 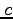 ?
?
4 (30 Pts) Each 15 points.
- Write the expression to economize the the Maclaurin series for
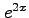 with the precision 0.008 by using Chebyshev polynomials. Do not perform the calculation.
with the precision 0.008 by using Chebyshev polynomials. Do not perform the calculation.
- Fourier series
- xvii
- Find the Fourier coefficients for
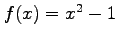 if it is periodic and one period extends from
if it is periodic and one period extends from 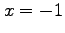 to
to 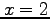 . Do not evaluate the integrals.
. Do not evaluate the integrals.
- xviii
- Write the Fourier series expansion for this function up to
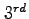 term.
term.
2006-09-28