Mcs 331 Numerical Methods
Midterm
Dec 06, 2013 10.40-12.30
Good Luck!
Solve all the questions. Each question is 25 pts.
-
This nonlinear equation is solved by using three methods, namely Bisection, Newton's, Muller's methods. Then, the following tables are obtained.
| iteration |
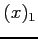 |
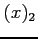 |
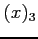 |
| 1 |
0.50000000000000 |
0.33333333333333 |
0.50000000000000 |
| 2 |
0.25000000000000 |
0.36017071357763 |
0.35491389049015 |
| 3 |
0.37500000000000 |
0.36042168047602 |
0.36046467792776 |
| 4 |
0.31250000000000 |
0.36042170296032 |
0.36042169766326 |
| 5 |
0.34375000000000 |
0.36042170296032 |
0.36042170296032 |
| iteration |
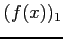 |
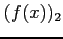 |
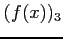 |
| 1 |
3.3070e-01 |
-1.0000e+00 |
3.3070e-01 |
| 2 |
-2.8662e-01 |
-6.8418e-02 |
-1.3807e-02 |
| 3 |
3.6281e-02 |
-6.2799e-04 |
1.0751e-04 |
| 4 |
-1.2190e-01 |
-5.6252e-08 |
-1.3252e-08 |
| 5 |
-4.1956e-02 |
-6.6613e-16 |
2.2204e-16 |
- i
- If the exact value is given as
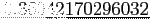 , fill the following tables (use scientific notation as %12.4e, see the table above);
, fill the following tables (use scientific notation as %12.4e, see the table above);
- ii
- Analyze the obtained tables. Is the convergence sustained for the each methods? For the sustained ones; at which iteration and why?
- iii
- What can you say about the speed of convergences for each method?
- iv
- By using your answers for the previous items, fill the following table. You should explain your decision.
- v
- Which method is the best one? Why?
- Consider the function:
Plot of the function is given at the following figure;
Figure 1:
Plot of the function, 2*x-6*log(x)
|
|
- vi
- Use two iterations of Newton's method to estimate only one of the roots of this function.
Hint:
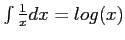
- vii
- Estimate the error in your answer to part i.
- viii
- Approximately how many iterations of the bisection method would have been required to achieve for the error value of 0.0004?
Hint: Take the interval as ((initial+1)-initial)
- Solve this system by Gaussian elimination with pivoting
- ix
- How many row interchanges are needed?
- x
- Repeat without any row interchanges. Do you get the same results?
- xi
- You could have saved the row multipliers and obtained a
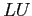 equivalent of the coefficient matrix. Use this
equivalent of the coefficient matrix. Use this 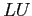 to solve but with right-hand sides of
to solve but with right-hand sides of ![$[-3,7,-2]^T$](img23.png)
- Consider the linear system
- xii
- Solve this system with the Jacobi method. First rearrange to make it diagonally dominant if possible. Use
![$[0,0,0]$](img25.png) as the starting vector.
as the starting vector.
- xiii
- Repeat with Gauss-Seidel method. Compare with Jacobi method.
Cem Ozdogan
2013-12-22
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 &-2 &4&6\\
8 &-3 &2&2\\
-1 &10 &2&4\\
\end{array} \right]
\end{displaymath}](img21.png)