Mcs 331 Numerical Methods
Midterm
Dec 06, 2013 10.40-12.30
Good Luck!

Solve all the questions. Each question is 25 pts.

1. 
   
   $$f(x)=3*x+sin(x)- e^x$$
   
   
   This nonlinear equation is solved by using three methods, namely Bisection, Newton's, Muller's methods. Then, the following tables are obtained.
   

   iteration	$(x)_1$	$(x)_2$	$(x)_3$
   1	0.50000000000000	0.33333333333333	0.50000000000000
   2	0.25000000000000	0.36017071357763	0.35491389049015
   3	0.37500000000000	0.36042168047602	0.36046467792776
   4	0.31250000000000	0.36042170296032	0.36042169766326
   5	0.34375000000000	0.36042170296032	0.36042170296032

   
   

   iteration	$(f(x))_1$	$(f(x))_2$	$(f(x))_3$
   1	3.3070e-01	-1.0000e+00	3.3070e-01
   2	-2.8662e-01	-6.8418e-02	-1.3807e-02
   3	3.6281e-02	-6.2799e-04	1.0751e-04
   4	-1.2190e-01	-5.6252e-08	-1.3252e-08
   5	-4.1956e-02	-6.6613e-16	2.2204e-16

   i

   If the exact value is given as $0.36042170296032$, fill the following tables (use scientific notation as %12.4e, see the table above);
   

   iteration	$Error_1$	$Error_2$	$Error_3$
   1
   2
   3
   4
   5

   $Error Ratio_1$	$Error Ratio_2$	$Error Ratio_3$

   
   

   iteration	$Error_1$	$Error_2$	$Error_3$
   1	1.3958e-01	-2.7088e-02	1.3958e-01
   2	-1.1042e-01	-2.5099e-04	-5.5078e-03
   3	1.4578e-02	-2.2484e-08	4.2975e-05
   4	-4.7922e-02	-1.6653e-16	-5.2971e-09
   5	-1.6672e-02	1.1102e-16	2.2204e-16

   $Error Ratio_1$	$Error Ratio_2$	$Error Ratio_3$
   7.1644e+00	-3.6916e+01	7.1644e+00
   -1.2640e+00	1.0793e+02	-2.5342e+01
   -7.5744e+00	1.1163e+04	-1.2816e+02
   -3.0421e-01	1.3501e+08	-8.1130e+03
   2.8744e+00	-1.5000e+00	-2.3856e+07

   ii

   Analyze the obtained tables. Is the convergence sustained for the each methods? For the sustained ones; at which iteration and why?
   First method does not converge, while the second method converges faster than the third one. The second method converges at the fourth step because the next step is also at the same error level and they are small enough. The third one seems to converge at the fifth step since it is small enough.

   iii

   What can you say about the speed of convergences for each method?
   From the error ratio table, first method has a monotonic behavior and it is also seen that it does not converge. The second method is the fastest method and it approaches to the exact value with the square of the error of the previous step in each iteration. The third one is also fast method but with the same ratio of the previous step.

   iv

   By using your answers for the previous items, fill the following table. You should explain your decision.
   

   	$Method_1$	$Method_2$	$Method_3$
   Name

   
   

   	$Method_1$	$Method_2$	$Method_3$
   Name	Bisection	Newton	Muller

   
   Bisection; since it halves at each iteration.
   Newton; since it converges quadratically.
   Muller; since is is the remaining one.

   v

   Which method is the best one? Why?
   Since we do not care about the prices for each method, dealing just with the numbers. Newton's method is the best one since it converges quadratically, so it is the fastest one.

2. Consider the function:
   
   $$f(x) = 2x-6log(x)$$
   
   
   Plot of the function is given at the following figure;

   Figure 1: Plot of the function, 2*x-6*log(x)

   

   vi

   Use two iterations of Newton's method to estimate only one of the roots of this function. Hint: $\int \frac{1}{x}dx=log(x)$
   Newton's method uses the algorithm
   

   $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$

   
   

   where, for this function
   

   $$f'(x)=2-6/x$$

   
   

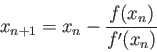
   >>solve('2*x-6*log(x)')
   ans = 
       -3*lambertw(-1/3)
    -3*lambertw(-1,-1/3)
   >> -3*lambertw(-1/3)
   ans =    1.8572
   >>  -3*lambertw(-1,-1/3)
   ans =    4.5364
   write the function
   function fx=func(x)
   fx=2*x-6*log(x);
   save as func.m
   write the function
   function fx=funcdiff(x)
   fx=2-6/x;
   save as funcdiff.m
   

   
   

   $$x_0 = 1.5$$

   
   

   >> format long
   >> x0=1.5;x1=x0-(func(x0)/funcdiff(x0))
   x1 =   1.78360467567551
   >> x2=x1-(func(x1)/funcdiff(x1))
   x2 =   1.85354064971539
   >> x3=x2-(func(x2)/funcdiff(x2))
   x3 =   1.85717450334217
   >> x4=x3-(func(x3)/funcdiff(x3))
   x4 =   1.85718386014596
   >> x5=x4-(func(x4)/funcdiff(x4))
   x5 =   1.85718386020784
   >> x6=x5-(func(x5)/funcdiff(x5))
   x6 =   1.85718386020784
   >> x7=x6-(func(x6)/funcdiff(x6))
   x7 =   1.85718386020784
   

   or start with
   

   $$x_0 = 3.1$$

   
   

   >> x0=3.1;x1=x0-(func(x0)/funcdiff(x0))
   x1 =  12.22039636867234
   >> x2=x1-(func(x1)/funcdiff(x1))
   x2 =   5.97649660388231
   >> x3=x2-(func(x2)/funcdiff(x2))
   x3 =   4.74567026655091
   >> x4=x3-(func(x3)/funcdiff(x3))
   x4 =   4.54457398303521
   >> x5=x4-(func(x4)/funcdiff(x4))
   x5 =   4.53641793698142
   >> x6=x5-(func(x5)/funcdiff(x5))
   x6 =   4.53640365501743
   >> x7=x6-(func(x6)/funcdiff(x6))
   x7 =   4.53640365497353
   >> x8=x7-(func(x7)/funcdiff(x7))
   x8 =   4.53640365497353
   >> x9=x8-(func(x8)/funcdiff(x8))
   x9 =   4.53640365497353
   

   vii

   Estimate the error in your answer to part i.
   To estimate the error, compute one more iteration (fourth iteration),
   

   $$x_0 = 1.5$$

   
   

   
   

   $$e_3 = x_4-x_3 = (1.85718386014596) - (1.85717450334217) = 9.356803789994927e-06$$

   
   

   or start with
   

   $$x_0 = 3.1$$

   
   

   
   

   $$e_3 = x_4-x_3 = (4.74567026655091) - (5.97649660388231) = -1.23082633733140$$

   
   

   viii

   Approximately how many iterations of the bisection method would have been required to achieve for the error value of 0.0004?
   Hint: Take the interval as ((initial+1)-initial)
   The error in the bisection method satisfies
   

   $$e_n=\vert\frac{Original~Interval}{2^n} \vert$$

   
   

   $x_0 = 1.5$ In this case, taking the original interval to be [1.5, 2.5], we would have
   

   $$e_n=\vert \frac{1}{2^n×} \vert$$

   
   

   Therefore, to achieve approximately the same error as we obtained with two iteration of Newton's method here, would require sufficient iterations of bisection to ensure
   

   $$\frac{1}{2^n}=0.0004$$

   
   

   this gives
   

   $$\frac{1}{0.0004}=e^{nln(2)}$$

   
   

   
   

   $$\frac{ln(\frac{1}{0.0004})}{ln(2)}=n$$

   
   

   
   

   $$n=12$$

   
   

   $x_0 = 3.1$

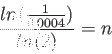
   same result.

3. Solve this system by Gaussian elimination with pivoting
   
   $$\left[ \begin{array}{rrrr} 1 &-2 &4&6\\ 8 &-3 &2&2\\ -1 &10 &2&4\\ \end{array} \right]$$
   
   

   ix

   How many row interchanges are needed?

   x

   Repeat without any row interchanges. Do you get the same results?

   xi

   You could have saved the row multipliers and obtained a $LU$ equivalent of the coefficient matrix. Use this $LU$ to solve but with right-hand sides of $[-3,7,-2]^T$

   Answer:

    %**********************************************
    %i) Ax=b
    >> A=[1 -2 4; 8 -3 2; -1 10 2]
    >> b=[6 2 4]
    >> GEPivShow(A,b')
    Begin forward elimination with Augmented system:
         1    -2     4     6
         8    -3     2     2
        -1    10     2     4
    Swap rows 1 and 2;  new pivot = 8
    After elimination in column 1 with pivot = 8.000000
        8.0000   -3.0000    2.0000    2.0000
             0   -1.6250    3.7500    5.7500
             0    9.6250    2.2500    4.2500
    Swap rows 2 and 3;  new pivot = 9.625
    After elimination in column 2 with pivot = 9.625000
        8.0000   -3.0000    2.0000    2.0000
             0    9.6250    2.2500    4.2500
             0         0    4.1299    6.4675
    ans =   -0.1132     0.0755     1.5660 %these are x1, x2, x3
    >> det(A)
    ans =   318
    >> 8.0000*9.6250 *4.1299 %product of the diagonal of U
    ans =  318.0023
    % For LU-decomposition
    >> [L,U,pv] = luPiv(A)
    L =    1.0000         0         0
            -0.1250    1.0000         0
             0.1250   -0.1688    1.0000
    U =   8.0000   -3.0000    2.0000
             0    9.6250    2.2500
             0         0    4.1299
    pv =
         2
         3
         1
    % two times pivoting
    %**********************************************
    % ii) for not pivoting case;
    >> GEshow(A,b')
    Begin forward elimination with Augmented system:
         1    -2     4     6
         8    -3     2     2
        -1    10     2     4
    After elimination in column 1 with pivot = 1.000000
         1    -2     4     6
         0    13   -30   -46
         0     8     6    10
    After elimination in column 2 with pivot = 13.000000
        1.0000   -2.0000    4.0000    6.0000
             0   13.0000  -30.0000  -46.0000
             0         0   24.4615   38.3077
    ans =    -0.1132     0.0755    1.5660
    >> 1.0000*13.0000*24.4615
    ans =   317.9995
    % Solutions are the same. They are same because the system is 
    % not ill-conditioned.
    %**********************************************
    % iii) LUx=bb now bb=[-3 7 -2] 
    % First Check!
    % L an U is found above. Coution: b --> Permutted b
    % b=[2 4 6]
    % Ly=b : Find y
    >> y=GEPivShow(L,b')
    Begin forward elmination with Augmented system:
       1.000000000000000                   0                   0   2.000000000000000
      -0.125000000000000   1.000000000000000                   0   4.000000000000000
       0.125000000000000  -0.168831168831169   1.000000000000000   6.000000000000000
    After elimination in column 1 with pivot = 1.000000
       1.000000000000000                   0                   0   2.000000000000000
                       0   1.000000000000000                   0   4.250000000000000
                       0  -0.168831168831169   1.000000000000000   5.750000000000000
    After elimination in column 2 with pivot = 1.000000
       1.000000000000000                   0                   0   2.000000000000000
                       0   1.000000000000000                   0   4.250000000000000
                       0                   0   1.000000000000000   6.467532467532467
    y =
       2.000000000000000
       4.250000000000000
       6.467532467532467
    % Ux=y : Find x
    >> xx=GEPivShow(U,y)
    Begin forward elmination with Augmented system:
       8.000000000000000  -3.000000000000000   2.000000000000000   2.000000000000000
                       0   9.625000000000000   2.250000000000000   4.250000000000000
                       0                   0   4.129870129870130   6.467532467532467
    After elimination in column 1 with pivot = 8.000000
       8.000000000000000  -3.000000000000000   2.000000000000000   2.000000000000000
                       0   9.625000000000000   2.250000000000000   4.250000000000000
                       0                   0   4.129870129870130   6.467532467532467
    After elimination in column 2 with pivot = 9.625000
       8.000000000000000  -3.000000000000000   2.000000000000000   2.000000000000000
                       0   9.625000000000000   2.250000000000000   4.250000000000000
                       0                   0   4.129870129870130   6.467532467532467
    xx =
      -0.113207547169811
       0.075471698113208
       1.566037735849056
    % Same as before as expected! 
    % Now for bb=[-3 7 -2]
    >> bb=[-3 7 -2]
    bb =    -3     7    -2
   >> y=GEPivShow(L,bb')
   Begin forward elmination with Augmented system:
      1.000000000000000                   0                   0  -3.000000000000000
     -0.125000000000000   1.000000000000000                   0   7.000000000000000
      0.125000000000000  -0.168831168831169   1.000000000000000  -2.000000000000000
   After elimination in column 1 with pivot = 1.000000
      1.000000000000000                   0                   0  -3.000000000000000
                      0   1.000000000000000                   0   6.625000000000000
                      0  -0.168831168831169   1.000000000000000  -1.625000000000000
   After elimination in column 2 with pivot = 1.000000
      1.000000000000000                   0                   0  -3.000000000000000
                      0   1.000000000000000                   0   6.625000000000000
                      0                   0   1.000000000000000  -0.506493506493507
   y =
     -3.000000000000000
      6.625000000000000
     -0.506493506493507
   >> xx=GEPivShow(U,y)
   Begin forward elmination with Augmented system:
      8.000000000000000  -3.000000000000000   2.000000000000000  -3.000000000000000
                      0   9.625000000000000   2.250000000000000   6.625000000000000
                      0                   0   4.129870129870130  -0.506493506493507
   After elimination in column 1 with pivot = 8.000000
      8.000000000000000  -3.000000000000000   2.000000000000000  -3.000000000000000
                      0   9.625000000000000   2.250000000000000   6.625000000000000
                      0                   0   4.129870129870130  -0.506493506493507
   After elimination in column 2 with pivot = 9.625000
      8.000000000000000  -3.000000000000000   2.000000000000000  -3.000000000000000
                      0   9.625000000000000   2.250000000000000   6.625000000000000
                      0                   0   4.129870129870130  -0.506493506493507
   xx =
     -0.075471698113208
      0.716981132075472
     -0.122641509433962  
    % solution is completed
    %**********************************************
     

4. Consider the linear system
   
   $$\begin{array}{r} 7x_1-3x_2+4x_3=6\\ -3x_1+2x_2+6x_3=2\\ 2x_1+5x_2+3x_3=-5\\ \end{array}$$
   
   

   xii

   Solve this system with the Jacobi method. First rearrange to make it diagonally dominant if possible. Use $[0,0,0]$ as the starting vector.

   xiii

   Repeat with Gauss-Seidel method. Compare with Jacobi method.

   Answer:

    %**********************************************
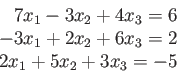
    %Switching rows 2 &3 first
    >> A=[7 -3 4; 2 5 3; -3 2 6]
    >> B=[6  -5 2]
    >> jacobi(A,B',P',0.01,20)
   k =     1 P =
      0.857142857142857
     -1.000000000000000
      0.333333333333333
   k =     2 P =
      0.238095238095238
     -1.542857142857143
      1.095238095238095
   k =     3 P =
     -0.429931972789116
     -1.752380952380953
      0.966666666666667
   k =     4 P =
     -0.446258503401361
     -1.408027210884354
      0.702494331065760
   k =     5 P =
     -0.147722708130871
     -1.242993197278911
      0.579546485260771
   k =     6 P =
     -0.006737933268545
     -1.288638807904114
      0.673803045027535
   k =     7 P =
     -0.080161229117497
     -1.401586653709102
      0.759510636000432
   k =     8 P =
     -0.177543215018434
     -1.423641889953260
      0.760448270010952
   k =     9 P =
     -0.187531249986227
     -1.385251675999198
      0.719109022475203
   k =    10 P =
     -0.147455873985486
     -1.356452913490631
      0.701318267006619
   k =    11 P =
     -0.124947401214053
     -1.361808610609777
      0.711756367504134
   k =   12 P =
     -0.133207328835124
     -1.377074860016859
      0.724795836262899
   k =    13 P =
     -0.147201132157454
     -1.381594570223690
      0.725754622254725
   k =    14 P =
     -0.149686028527138
     -1.376572320489853
      0.720264290662503
   k =    15 P =
     -0.144396303445653
     -1.372284162986646
      0.717347759233048
   k =    16 P =
     -0.140891932270305
     -1.372650134161568
      0.718563235939389
   k =    17 P =
     -0.141743335177466
     -1.374781168655511
      0.720437411918703
   k =    18 P =
     -0.143727593377335
     -1.375565113080236
      0.720722055296438
   k =    19 P =
     -0.144226222918065
     -1.374942195826928
      0.719991241004744
    >> gseid(A,B',P',0.001,20)
   k =        1   P =
         0.857142857142857
        -1.342857142857143
         1.209523809523809
   k =        2   P =
        -0.409523809523810
        -1.561904761904762
         0.649206349206349
   k =        3   P =
        -0.183219954648526
        -1.316235827664399
         0.680468631897203
   k =        4   P =
        -0.095797430083144
        -1.369962207105064
         0.742088687326783
   k =        5   P =
        -0.154034481517475
        -1.383639419789080
         0.717529232504289
   k =        6   P =
        -0.145862169912057
        -1.372172671537751
         0.717793138889889
   k =        7   P =
        -0.141098652881830
        -1.374236422181201
         0.720862814286152
   k =        8   P =
        -0.143737217669745
        -1.375022801503793
         0.719805658333059
   k =        9   P =
        -0.143470148263374
        -1.374495335694486
         0.719763371099808
   % Gauss-Seidel iterates much faster