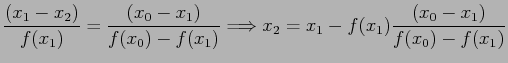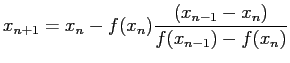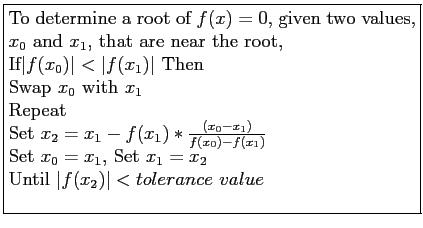The Secant Method

• Bisection is simple to understand but it is not the most efficient way to find where 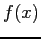$f(x)$ is zero.
• Most functions can be approximated by a straight line over a small interval.

Figure 3.4: Graphical illustration of the Secant Method.

• The secant method begins by finding two points on the curve of 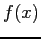$f(x)$, hopefully near to the root.
• As Figure 3.4 illustrates, we draw the line through these two points and find where it intersects the x-axis.
• If 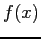$f(x)$ were truly linear, the straight line would intersect the x-axis at the root.

• The intersection of the line with the x-axis is not at 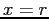$x=r$ (root) but it should be close to it.
• From the obvious similar triangles we can write
  $$\frac{(x_1 - x_2)}{f(x_1)}=\frac{ (x_0 - x_1)}{f(x_0) - f(x_1)}\Longrightarrow x_2=x_1-f(x_1)\frac{(x_0-x_1)}{f(x_0)-f(x_1)}$$

• Because f(x) is not exactly linear, 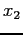$x_2$ is not equal to $r$,
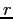• but it should be closer than either of the two points we began with. If we repeat this, we have:
  $$x_{n+1}=x_n-f(x_n)\frac{(x_{n-1}-x_n)}{f(x_{n-1})-f(x_n)}$$

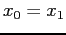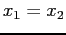• The net effect of this rule is to set $x_0 =x_1$ and $x_1=x_2$, after each iteration.

• The technique we have described is known as, the secant method because the line through two points on the curve is called the secant line.
• An algorithm for the Secant Method:
  

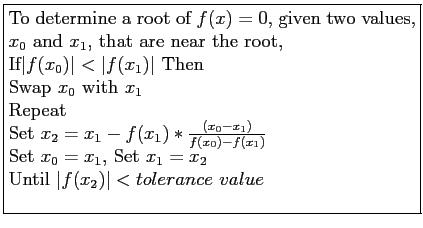
Table 3.2: The Secant method for 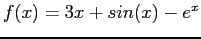$f(x)=3x + sin(x) - e^x$, starting from 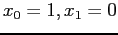$x_0=1,x_1=0$, using a tolerance value of 1E-6.

• Table 3.2 shows the results from the secant method for the same function that was used to illustrate bisection.
• An alternative stopping criterion for the secant method is when the pair of points being used are sufficiently close together.
• If the method is being carried out by a program that displays the successive iterates, the user can interrupt the program should such improvident behavior be observed.
• If 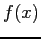$f(x)$ is not continuous, the method may fail.

• If the function is far from linear near the root, the successive iterates can fly off to points far from the root, as seen if Fig. 3.5.

  Figure 3.5: A pathological case for the secant method.

  
• If the function was plotted before starting the method, it is unlikely that the problem will be encountered, because a better starting value would be used.