- The fixed-point method converges at a linear rate;
- it is said to be linearly convergent, meaning that the error at each successive iteration is a constant fraction of the previous error.
Table 3.4:
The order of convergence for the iteration algorithm with the different forms of 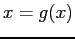 .
.
![\begin{table}
\begin{center}
\includegraphics[scale=0.6]{figures/1-24}
\end{center}\end{table}](img330.png) |
- If we tabulate the errors after each step in getting the roots of the polynomial and its ratio to the previous error,
- we find that the magnitudes of the ratios to be levelling out at 0.3333. (See Table 3.4)
- Example: Comparing Muller's and Fixed-point Iteration methods (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/mainmulfix.m m-files: mainmulfix.m, http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/muller.m muller.m, http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/fixedpoint.m fixedpoint.m)
Cem Ozdogan
2011-12-27