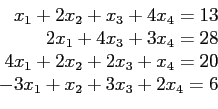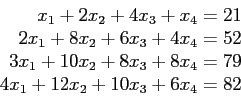Upper Triangularization Followed by Back Substitution. To construct the solution to 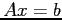 , by first reducing the augmented matrix
, by first reducing the augmented matrix ![$ [A\vert b]$](img507.png) to upper-triangular form then performing back substitution.
to upper-triangular form then performing back substitution.
- reducing the augmented matrix
![$ [A\vert b]$](img507.png) to upper-triangular form; http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter2/uptrbk.m uptrbk.m.
to upper-triangular form; http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter2/uptrbk.m uptrbk.m.
- back substitution; http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter2/backsub.m backsub.m.
Analyze these MATLAB codes, then by using these codes solve the following linear system;
Solution:
save with the names http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter2/uptrbk.muptrbk.m and http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter2/backsub.mbacksub.m. Then;
>> A=[? ? ? ?;? ? ? ?;? ? ? ?;? ? ? ?]
>> B=[? ? ? ?]'
>> uptrbk(A,B)