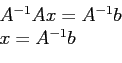The Inverse of a Matrix and Matrix Pathology
- Division by a matrix is not defined but the equivalent is obtained from the inverse of the matrix.
- If the product of two square matrices,
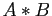 , equals to the identity matrix,
, equals to the identity matrix, 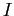 ,
, 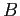 is said to be the inverse of
is said to be the inverse of 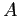 (and also
(and also 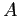 is the inverse of
is the inverse of 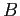 ).
).
- Matrices do not commute (
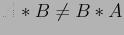 ) on multiplication but inverses are an exception:
) on multiplication but inverses are an exception:
 .
.
- To find the inverse of matrix
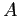 , use an elimination method.
, use an elimination method.
- We augment the
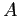 matrix with the identity matrix of the same size and solve. The solution is
matrix with the identity matrix of the same size and solve. The solution is 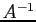 . Example;
. Example;
- Cont.
- We confirm the fact that we have found the inverse by multiplication:
- It is more efficient to use Gaussian elimination. We show only the final triangular matrix; we used pivoting:
- After doing the back-substitutions, we get
- If we have the inverse of a matrix, we can use it to solve a set of equations,
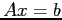 ,
,
- because multiplying by
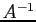 gives the answer (
gives the answer (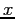 ):
):
Subsections
Cem Ozdogan
2011-12-27
![\begin{displaymath}
A=\left[
\begin{array}{rrr}
1 & -1 & 2 \\
3 & 0 & 1 \\
1 & 0 & 2 \\
\end{array} \right],
\end{displaymath}](img537.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & -1 & 2 & 1 &0 & 0\\
3 & 0 & 1 & 0 &1 & 0\\
1 & 0 & 2 & 0 &0 & 1\\
\end{array} \right],
\end{displaymath}](img538.png)
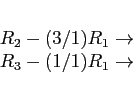
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & -1 & 2 & 1 &0 & 0\\
0 & 3 &-5 &-3 &1 & 0\\
0 & 1 & 0 &-1&0 & 1\\
\end{array} \right],
\end{displaymath}](img540.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & -1 & 2 & 1 &0 & 0\\
0 & 1 & 0 &-1&0 & 1\\
0 & 3 &-5 &-3 &1 & 0\\
\end{array}\right],
\end{displaymath}](img541.png)
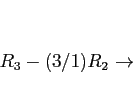
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & -1 & 2 & 1 &0 & 0\\
0 & 1 & 0 &-1&0 & 1\\
0 & 0 &-5 & 0 &1 &-3\\
\end{array}\right],
\end{displaymath}](img543.png)
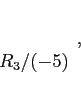
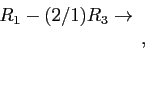
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & -1 & 0 & 1 &2/5&-6/5\\
0...
... 0 &-1&0 & 1\\
0 & 0 &1 & 0 &-1/5&3/5\\
\end{array}\right],
\end{displaymath}](img546.png)
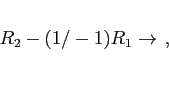
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & 0 & 0 & 0 &2/5&-1/5\\
0 ...
...& 0 &-1&0 & 1\\
0 & 0 &1 & 0 &-1/5&3/5\\
\end{array}\right]
\end{displaymath}](img548.png)
![\begin{displaymath}
\underbrace{\left[
\begin{array}{rrr}
1 & -1 & 2 \\
3 & 0 & 1 \\
1 & 0 & 2 \\
\end{array} \right]}_A*
\end{displaymath}](img549.png)
![\begin{displaymath}
\underbrace{\left[
\begin{array}{rrr}
0 &2/5&-1/5\\
-1&0 & 1\\
0 &-1/5&3/5\\
\end{array} \right]}_{A^{-1}}=
\end{displaymath}](img550.png)
![\begin{displaymath}
\underbrace{\left[
\begin{array}{rrr}
1 & 0 & 0\\
0 & 1 & 0 \\
0 & 0 &1 \\
\end{array} \right]}_I
\end{displaymath}](img551.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
1 & -1 & 2 & 1 &0 & 0\\
3 & ...
...
(0.333) & (0) & 1.667 & 0 &-0.333 & 1\\
\end{array} \right]
\end{displaymath}](img552.png)
![\begin{displaymath}
\left[
\begin{array}{rrrrrr}
3 & 0 & 1 & 0 &0.4& -0.2\\
(...
...
(0.333) & (0) & 1.667 & 0 &-0.2 & 0.6\\
\end{array} \right]
\end{displaymath}](img553.png)