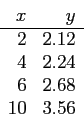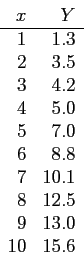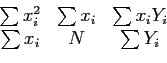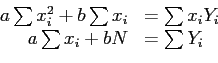Hands-on-Interpolation and Curve Fitting with MATLAB I

1. For the given data points;
   $$\begin{array}{rr} x & y \hline 2 & 2.12 \\ 4 & 2.24 \\ 6 & 2.68 \\ 10 & 3.56 \\ \end{array}$$
   • Study this example in MATLAB; $Start \Rightarrow Toolboxes \Rightarrow CurveFitting \Rightarrow Curve  Fitting  Tool$.
   • Fit to linear polynomial, quadratic polynomial, cubic polynomial.
   • For each polynomial;
     • interpolate for $x=5$
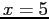
     • extrapolate for $x=12$
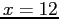
   • Compare your results, which one is the best? Why?
2. For the given data points;
   $$\begin{array}{rr} x & Y \hline 1 & 1.3\\ 2 & 3.5\\ 3 & ... ...\\ 7 & 10.1\\ 8 & 12.5\\ 9 & 13.0\\ 10& 15.6\\ \end{array}$$

   i

   Plot it (such as plot(x,Y,'o')).

   ii

   The graph suggest a linear relationship.

   $$y=ax + b$$

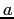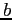   values for the parameters, $a$ and $b$, can be obtained from the plot.

   iii

   Write a MATLAB code that calculates each summation;

   $$\begin{array}{ccc} \sum x_i^2 & \sum x_i & \sum x_iY_i\\ \sum x_i & N & \sum Y_i\\ \end{array}$$

   All the summations are from 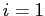$i= 1$ to $i= N$.

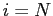   iv

   Then it is obtained as

   $$\begin{array}{rl} a\sum x_i^2+b\sum x_i & =\sum x_iY_i\\ a\sum x_i+bN & =\sum Y_i\\ \end{array}$$

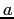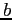   Solving these equations simultaneously gives the values for slope and intercept $a$ and $b$. Now, we have a function in the form;

   $$y=ax + b$$

   v

   Plot them (such as plot(x,y,x,Y,'o')).