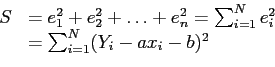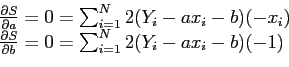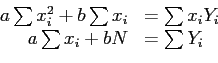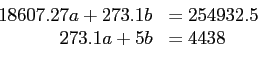Least-Squares Approximations
- Until now, we have assumed that the data are accurate,
- but when these values are derived from an experiment, there is some error in the measurements.
Figure 5.6:
Resistance vs Temperature graph for the Least-Squares Approximation.
|
|
- Some students are assigned to find the effect of temperature on the resistance of a metal wire.
- They have recorded the temperature and resistance values in a table and have plotted their findings, as seen in Fig. 5.6.
- The graph suggest a linear relationship.
- Values for the parameters,
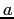 and
and 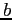 , can be obtained from the plot.
, can be obtained from the plot.
- If someone else were given the data and asked to draw the line,
- it is not likely that they would draw exactly the same line and they would get different values for
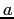 and
and 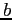 .
.
- In analyzing the data, we will assume that the temperature values are accurate
- and that the errors are only in the resistance numbers; we then will use the vertical distances.
- A way of fitting a line to experimental data that is to minimize the deviations of the points from the line.
- The usual method for doing this is called the least-squares method.
- The deviations are determined by the distances between the points and the line.
Figure 5.7:
Minimizing the deviations by making the sum a minimum.
|
|
- Consider the case of only two points (See Fig. 5.7).
- Obviously, the best line passes through each point,
- but any line that passes through the midpoint of the segment connecting them has a sum of errors equal to zero.
- We might first suppose we could minimize the deviations by making their sum a minimum, but this is not an adequate criterion.
- We might accept the criterion that we make the magnitude of the maximum error a minimum (the so-called minimax criterion).
- The usual criterion is to minimize the sum of the squares of the errors, the least-squares principle.
- In addition to giving a unique result for a given set of data, the least-squares method is also in accord with the maximum-likelihood principle of statistics.
- If the measurement errors have a so-called normal distribution
- and if the standard deviation is constant for all the data,
- the line determined by minimizing the sum of squares can be shown to have values of slope and intercept that have maximum likelihood of occurrence.
- Solving these equations simultaneously gives the values for slope and intercept
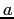 and
and 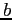 .
.
- For the data in Fig. 5.6 we find that
- Our normal equations are then
- From these we find
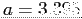 ,
, 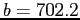 , and
, and
- MATLAB gets a least-squares polynomial with its polyfit command.
- When the numbers of points (the size of
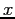 ) is greater than the degree plus one, the polynomial is the least squares fit.
) is greater than the degree plus one, the polynomial is the least squares fit.
Cem Ozdogan
2011-12-27