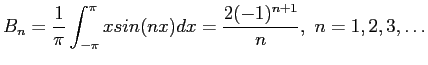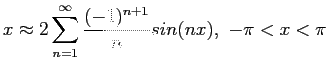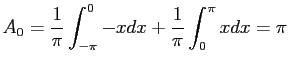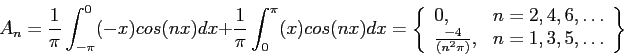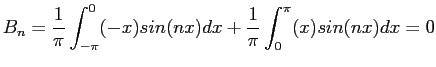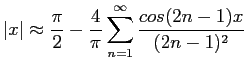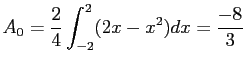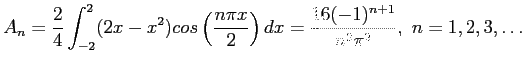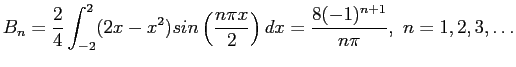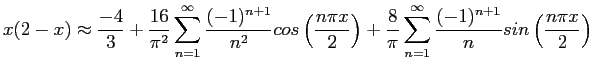Fourier Series for Periods Other Than 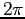
Figure 6.5:
Left: Plot of  , periodic of period
, periodic of period 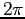 ,Right: Plot of the Fourier series expansion for
,Right: Plot of the Fourier series expansion for 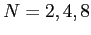 .
.
|
|
Examples:
- Let
 be periodic between
be periodic between 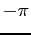 and
and 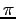 . (See Figure 6.5left). Find the
. (See Figure 6.5left). Find the  s and
s and 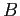 s of its Fourier expansion. For
s of its Fourier expansion. For 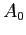 ;
;
For the other 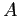 s;
s;
For the other 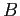 s;
s;
We then have
Figure 6.5right shows how the series approximates to the function when only two, four, or eight terms are used.
- Find the Fourier coefficients for
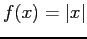 on
on 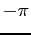 to
to 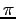 ;
;
Because the definite integrals are nonzero only for odd values of 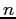 , it simplifies to change the index of the summation. The Fourier series is then
, it simplifies to change the index of the summation. The Fourier series is then
Figure 6.6 shows how the series approximates the function when two, four, or eight terms are used.
Figure 6.6:
Plot of Fourier series for 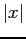 for
for 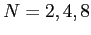 .
.
|
|
- Find the Fourier coefficients for
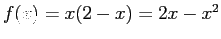 over the interval [-2, 2] if it is periodic of period 4. Equations 6.10 and 6.11 apply.
over the interval [-2, 2] if it is periodic of period 4. Equations 6.10 and 6.11 apply.
Figure 6.7 shows how the series approximates to the function when 40 terms are used.
Figure 6.7:
Plot of Fourier series for 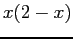 for
for 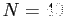 .
.
|
|
With MATLAB,
Cem Ozdogan
2011-12-27
![$\displaystyle A_0=\frac{1}{\pi}\int_{-\pi}^{\pi} f(x)dx=\frac{1}{\pi}\int_{-\pi}^{\pi} xdx=\left[ \frac{x^2}{2\pi}\right] ^{\pi}_{-\pi}=0
$](img1005.png)