- If we are working with experimental data that are displayed in a table of [
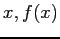 ] pairs emulation of calculus is impossible.
] pairs emulation of calculus is impossible.
- We must approximate the function behind the data in some way.
- Differentiation with a Computer:
- Employs the interpolating polynomials to derive formulas for getting derivatives.
- These can be applied to functions known explicitly as well as those whose values are found in a table.
- Numerical Integration-The Trapezoidal Rule:
- Approximates, the integrand function with a linear interpolating polynomial to derive a very simple but important formula for numerically integrating functions between given limits.
- We continue to exploit the useful properties of polynomials to develop methods for a computer to do integrations and to find derivatives.
- When the function is explicitly known, we can emulate the methods of calculus.
- But doing so in getting derivatives requires the subtraction of quantities that are nearly equal and that runs into round-off error.
- However, integration involves only addition, so round-off is not problem.
- We cannot often find the true answer numerically because the analytical value is the limit of the sum of an infinite number of terms.
- We must be satisfied with approximations for both derivatives and integrals but, for most applications, the numerical answer is adequate.
Subsections
Cem Ozdogan
2011-12-27