Nonlinear Systems
Figure 7:
A pair of equations.
|
|
- A pair of equations:
- Graphically, the solution to this system is represented by the intersections of the circle
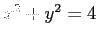 with the curve
with the curve 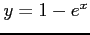 (see Fig. 7)
(see Fig. 7)
- Newton's method can be applied to systems as well as to a single nonlinear equation. We begin with the forms
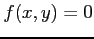 , , |
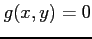 |
- Let
be a root.
- Expand both functions as a Taylor series about the point
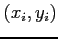 in terms of
in terms of
where 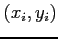 is a point near the root:
is a point near the root:
- Taylor series expansion of functions;
 Truncating both series gives
Truncating both series gives
 which we can rewrite as
which we can rewrite as
Example:
The partial derivatives are
 Beginning with
Beginning with
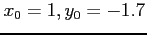 , we solve
, we solve
 This gives
This gives
| |
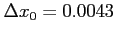 , , |
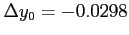 |
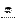 from which
from which
| |
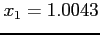 , , |
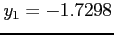 . . |
- These agree with the true value within 2 in the fourth decimal place. Repeating the process once more:
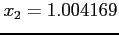 , , |
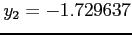 . . |
Then,
| f(1.004169,-1.729637)=-0.0000001, |
| g(1.004169,-1.729637)=-0.00000001, |
Subsections
Cem Ozdogan
2010-10-13
![]() Truncating both series gives
Truncating both series gives
![]() which we can rewrite as
which we can rewrite as
![]() Beginning with
Beginning with
![]() , we solve
, we solve
![]() This gives
This gives
![]() from which
from which