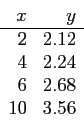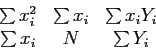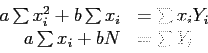- For the given data points;
- i
- construct the divided-difference table by hand
- ii
- run the MATLAB code (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter3/newpoly.m newpoly.m) and compare with your table.
- interpolate for

- extrapolate for

- iii
- run the MATLAB code (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter3/divDiffTable.m divDiffTable.m)
- interpolate for

- extrapolate for

Hint: Open these m-files with the editor. Then execute the codes according to the first line. Use these outputs to inter/extrapolate (see lecture notes).
- The MATLAB procedure for polynomial least-squares is polyfit. Study the following example;
- For the given data points;
T (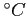 ) ) |
R (ohms) |
| 20.5 |
765 |
| 32.7 |
826 |
| 51.0 |
873 |
| 73.2 |
942 |
| 95.7 |
1032 |
- iv
- Plot it (such as plot(x,Y,'o')).
- v
- The graph suggest a linear relationship.
values for the parameters, 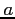 and
and 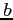 , can be obtained from the plot.
, can be obtained from the plot.
- vi
- Write a MATLAB code that calculates each summation;
All the summations are from 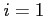 to
to 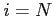 .
.
- vii
- Then it is obtained as
Solving these equations simultaneously gives the values for slope and intercept 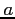 and
and 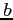 . Now, we have a function in the form;
. Now, we have a function in the form;
- viii
- Plot them (such as plot(x,y,x,Y,'o')).
Cem Ozdogan
2010-12-06