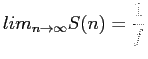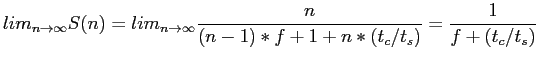Parallel Computation with Serial Sections Model

• It is assumed (or known) that a fraction 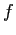$f$ of the given task (computation) is not dividable into concurrent subtasks.
• The remaining part 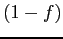$(1-f)$ is assumed to be dividable into concurrent subtasks.
• The time required to execute the task on 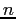$n$ processors is
  $$t_p=t_s*f+(1-f)*(t_s/n)$$

• The speed-up factor is therefore given by

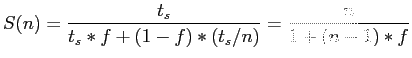  $$S(n)=\frac{t_s}{t_s*f+(1-f)*(t_s/n)}=\frac{n}{1+(n-1)*f}$$ (3.4)

  
  

• According to this equation, the potential speed-up due to the use of 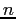$n$ processors is determined primarily by the fraction of code that cannot be divided.
• If the task (program) is completely serial, that is, 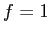$f=1$, then no speed-up can be achieved regardless of the number of processors used.

• This principle is known as Amdahl's law.
• It is interesting to note that according to this law, the maximum speed-up factor is given by
  $$lim_{n\rightarrow \infty} S(n)=\frac{1}{f}$$

• Therefore, the improvement in performance (speed) of a parallel algorithm over a sequential one is
  • limited not by the number of processors employed
  • but rather by the fraction of the algorithm that cannot be parallelized.
• According to Amdahl's law, researchers were led to believe that a substantial increase in speed-up factor would not be possible by using parallel architectures.
• NOT parallelizable;
  • communication overhead,
  • a sequential fraction, $f$

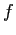
• The maximum speed-up factor under such conditions is given by

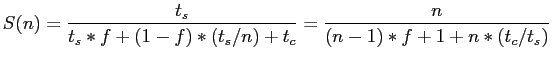  $$S(n)=\frac{t_s}{t_s*f+(1-f)*(t_s/n)+t_c}=\frac{n}{(n-1)*f+1+n*(t_c/t_s)}$$ (3.5)

  
  
  $$lim_{n\rightarrow \infty} S(n)=lim_{n\rightarrow \infty} \frac{n}{(n-1)*f+1+n*(t_c/t_s)}=\frac{1}{f+(t_c/t_s)}$$

• The above formula indicates that the maximum speed-up factor is determined not by the number of parallel processors employed but by the fraction of the computation that is not parallelized and the communication overhead.
• Recall that the efficiency is defined as the ratio between the speed-up factor and the number of processors, $n$.
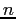• The efficiency can be computed as:

  $$\begin{array}{l} E(no communication overhead)=\frac{1}{1+(n-1... ...unication overhead)=\frac{1}{(n-1)*f+1+n*(t_c/t_s)} \end{array}$$ (3.6)

  
  

• As the number of processors increases, it may become difficult to use those processors efficiently.