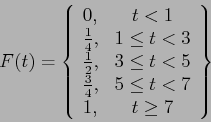Ceng 272 Statistical Computations
Final
June 02, 2011 11.30-12.30
Good Luck!
You are allowed to use CALCULATOR.
No any other electronic equipment is allowed.
Write the solutions explicitly and use the statistical terminology
Answer all the questions.
- Solve each questions
- i
- (5 pts) If an experiment consists of throwing a die and then drawing a letter at random from the English alphabet, how many points are there in the sample space?
- ii
- (10 pts) Drawing names out of a hat for a lottery. Don't put names back in if they get drawn. Suppose we have 60 students and we draw 3 names.
- (i)
- How many possible outcomes if we keep track of the order of names?
- (ii)
- How many set of 3 names are possible if the order they are drawn is ignored?
- iii
- (10 pts) If we flip two coins,
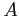 and
and 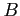 and it is given that
and it is given that 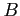 came up heads,
came up heads,
- (i)
- What is the probability that
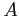 was head?
was head?
- (ii)
- Are these two events (
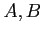 ) independent?
) independent?
- Solve each questions
- iv
- (10 pts) Determine the value
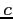 so that each of the following functions can serve as a probability distribution of the discrete random variable
so that each of the following functions can serve as a probability distribution of the discrete random variable  :
:
- (a)
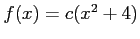 for
for 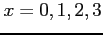
- (b)
-
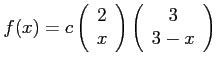 for
for 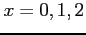 ,
,
- v
- (10 pts) An investment firm offers its customers municipal bonds that mature after varying numbers of years. Given that the cumulative distribution function of
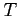 , the number of years to maturity for a randomly selected bond, is,
, the number of years to maturity for a randomly selected bond, is,
Find
- (a)
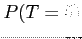
- (b)
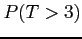
- (c)
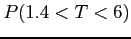
- (10 pts) Suppose that
 and
and 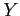 have the following joint probability function:
have the following joint probability function:
| |
|
x |
|
| |
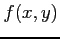 |
2 |
4 |
| |
1 |
0.10 |
0.15 |
| y |
3 |
0.20 |
0.30 |
| |
5 |
0.10 |
0.15 |
- (a)
- Find the expected value of
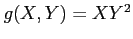 .
.
- (b)
- Find
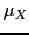 and
and 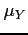 .
.
- (10 pts) It is known that 60% of mice inoculated with a serum are protected from a certain disease. If 5 mice are inoculated, find the probability that
- (a)
- none contracts the disease;
- (b)
- fewer than 2 contract the disease;
- (c)
- more than 3 contract the disease.
- (10 pts) To avoid detection at customs, a traveller places 6 narcotic tablets in a bottle containing 9 vitamin pills that are similar in appearance. If the customs official selects 3 of the tablets at random for analysis, what is the probability that the traveller will be arrested for illegal possession of narcotics
- (15 pts) In a nationwide test (High school), the scores,
 are normally distributed with
are normally distributed with 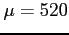 and
and  . Suppose a student's score is 680 in the test.
. Suppose a student's score is 680 in the test.
- (a)
- What percentage of the students of this test score between 480 and 620?
- (b)
- What fraction of students have a higher scores this student?
- (c)
- Suppose an university gives an admission to the students who gets top 15%. What is the minimum score to get an admission?
- (15 pts) Let
 and
and 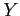 denote the position of an electron in the 2 dimensional Cartesian plane. Due to the uncertainty principle
denote the position of an electron in the 2 dimensional Cartesian plane. Due to the uncertainty principle  and
and 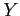 can't be measured exactly and are random variables. You are told that the measurement along the
can't be measured exactly and are random variables. You are told that the measurement along the  -axis is independent from the measurement along the
-axis is independent from the measurement along the 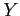 -axis. Furthermore, let
-axis. Furthermore, let  have a normal marginal density function with
have a normal marginal density function with 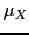 ,
, 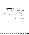 and let
and let 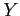 have a normal marginal density function with
have a normal marginal density function with 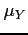 ,
, 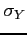 . What is the joint density function for
. What is the joint density function for  ,
, 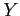 ? (Hints: for normal marginal density function
? (Hints: for normal marginal density function 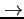
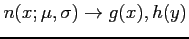 ; joint density function
; joint density function 
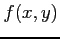 )
)
- (15 pts) The heights of 1000 students are approximately normally distributed with a mean of 174.5 centimetres and a standard deviation of 6.9 centimetres. If 200 random samples of size 25 are drawn from this population and the means recorded to the nearest tenth of a centimetre, determine
- (a)
- the mean and standard deviation of the sampling distribution of
 ;
;
- (b)
- the number of sample means that fall between 172.5 and 175.8 centimetres inclusive;
- (c)
- the number of sample means falling below 172.0 centimetres.
Cem Ozdogan
2011-06-15
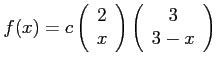 for
for