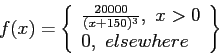Ceng 272 Statistical Computations
Midterm
Apr 06, 2011 14:40 - 16:30
Good Luck!
Answer all the questions.
Write the solutions explicitly and use the statistical terminology
- (5 pts) A rigged dice is known to have probability
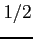 for the outcome 6 and all other outcomes are known to be equally likely. What is the probability for outcome 2?
for the outcome 6 and all other outcomes are known to be equally likely. What is the probability for outcome 2?
- (10 pts) Suppose we have a group of 5 candidates
- i
- Find the number of ways selecting 3 council members.
- ii
- Find the number of ways selecting chair, vice chair, and treasurer from the group of 5 candidates.
- (20 pts) Given that
- A: College graduate. B: Smoker. C: Heartdisease.
-
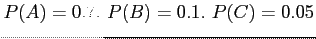
-
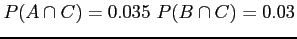
Find that
- iii
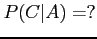 . Are these two events (
. Are these two events (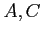 ) independent?
) independent?
- iv
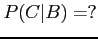 . Are these two events (
. Are these two events (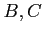 ) independent?
) independent?
- (15 pts) The shelf life, in days, for bottles of a certain prescribed medicine is a random variable having the density function
Find the probability that a bottle of this medicine will have a shell life of
- v
- at least 150 days;
- vi
- anywhere from 60 to 90 days.
- (15 pts) A private pilot wishes to insure his airplane for $200000. The insurance company estimates that a total loss may occur with probability 0.002, a 50% loss with probability 0.01, and a 25% loss with probability 0.1. Ignoring all other partial losses, what premium should the insurance company charge each year to realize an average profit of $500?
- (15 pts) Suppose that the probabilities are 0.4, 0.3, 0.2 and 0.1, respectively, that 0, 1, 2 and 3 power failures will strike a certain subdivision in any given year. Find the mean and variance of the random variable
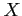 representing the number of power failures striking this subdivision.
representing the number of power failures striking this subdivision.
- (20 pts) Compute
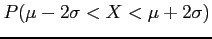 , where
, where 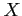 has the density function
has the density function
and compare with the result given in Chebyshev's theorem.
Cem Ozdogan
2011-04-11