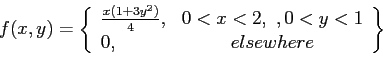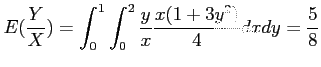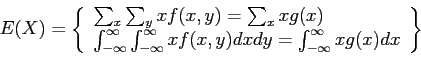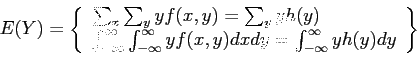- Suppose that a probability distribution of a random variable
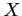 is specified.
is specified.
- For a measure of central tendency of the random variable
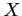 we use the terms expectation, expected value, and average value for the same concept.
we use the terms expectation, expected value, and average value for the same concept.
- Intuitively, the expected value of
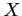 is the average value that the random variable takes on.
is the average value that the random variable takes on.
- However, some of the values of the random variable
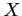 could be more (or less) probable than the other in the distribution unless the random variable is distributed uniformly.
could be more (or less) probable than the other in the distribution unless the random variable is distributed uniformly.
- Hence, in order to consider an average value of
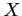 we need to take its probability into account.
we need to take its probability into account.
- Example: If two coins are tossed 16 times and
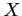 is the number of heads that occur per toss, then the value of
is the number of heads that occur per toss, then the value of 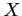 can be 0, 1, 2.
can be 0, 1, 2.
- The experiment yields no heads, one head, and two heads a total of 4, 7, and 5 times, respectively.
- The average number of heads per toss is then
where
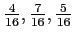 are relative frequencies
are relative frequencies
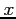 |
0 |
1 |
2 |
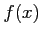 |
4/16 |
7/16 |
5/16 |
- Example 4.1: A lot contain 4 good components and 3 defective components.
- A sample of 3 is taken by a quality inspector.
- Find the expected value of the number of good components in this sample.
- Solution:
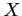 represents the number of good components
represents the number of good components
- Example 4.3: Let
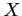 be the random variable that denotes the life in hours of a certain electronic device. The probability density function is as the following.
be the random variable that denotes the life in hours of a certain electronic device. The probability density function is as the following.
Find the expected life of this type of device.
- Solution:
- Theorem 4.1::
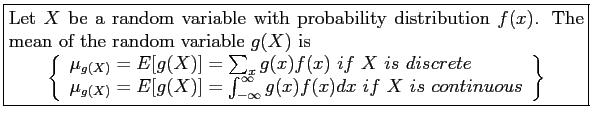
- Example 4.5: Let
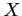 be a random variable with density function
be a random variable with density function
- Find the expected value of
 .
.
- Solution:
- Theorem 4.2::

- Example 4.7: Find
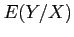 for the density function
for the density function
- Solution:
- If
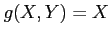 is
is
where 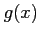 is the marginal distribution of
is the marginal distribution of 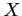
- If
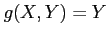 is
is
where 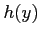 is the marginal distribution of
is the marginal distribution of 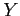
Cem Ozdogan
2010-03-25
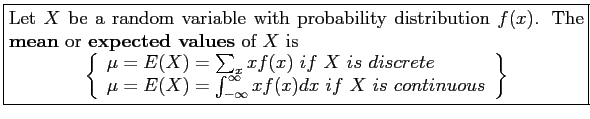
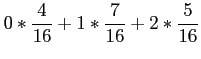
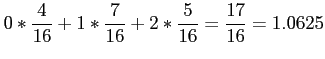
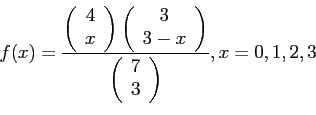
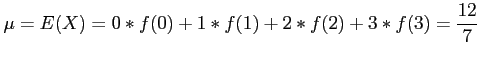
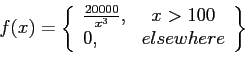
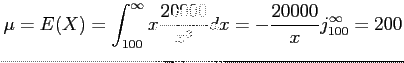
![\begin{displaymath}
\begin{array}{l}
P[g(X) = 0] = P(X = 0) = f(0), \\
P[g(X) =...
...f(-1)+ f(1), \\
P[g(X) = 4] = P(X = 2) = f(2), \\
\end{array}\end{displaymath}](img18.png)
![\begin{displaymath}
\begin{array}{rl}
E(g(X))& = 0*f(0)+1*[f(-1)+f(1)]+4*f(2) \\...
...(0)+(1)^2*f(1)+(2)^2*f(2) \\
& = \sum_x g(x)*f(x)
\end{array}\end{displaymath}](img21.png)
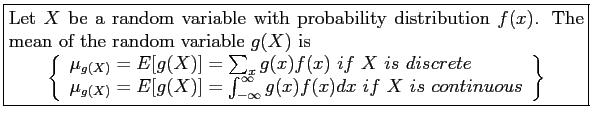
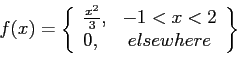
![$\displaystyle E[g(X)]=E(4X+3)=\frac{1}{3}\int_{-1}^2 (4x^3+3x^2)dx=8
$](img25.png)