- MATLAB (short for Matrix Laboratory) is a package designed for both practical computations
and theoretical investigations of numerical methods and computation. (As its name probably indicates, its original forte was matrix computations, however the current capabilities of MATLAB are far greater.) MATLAB is actually based on a complex suite of C programs that implement certain "primitive" subroutine operations, plus an interface driver routine which converts input "English-like" and mathematical expressions into the correct subroutine calls.
On most systems (including the PC's in the laboratory we shall use), MATLAB is started by "double-clicking" on the appropriate icon. After a brief delay, during which the program is loaded and a graphic displaying a surface plot flashes on the screen, the MATLAB welcome and the command prompt (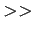 ) will appear. From here on, the user is free to create virtually any allowable algebraic, functional, or matrix operation or calculation by simply typing in the appropriate command.
) will appear. From here on, the user is free to create virtually any allowable algebraic, functional, or matrix operation or calculation by simply typing in the appropriate command.
>>(2+3*pi)/2
>>3*cos(sqrt(4.7))
>>format long
>>3*cos(sqrt(4.7))
- Assignment Statements
>>a=3-floor(exp(2.9))
>>b=sin(a);
>>2*b-2
- Defining Functions
Construct an m-file in the m-file Editor/Debugger (by selecting New under File ). Once defined, a user-defined function is called similarly as built-in functions.
Ex. Place the function
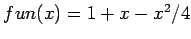 in the m-file fun.m. In the Editor/Debugger:
in the m-file fun.m. In the Editor/Debugger:
function y=fun(x)
y=1+x-x.^2/4; %(Why . ?)
Once this function is saved as an m-file
named fun.m,
>>cos(fun(3))
>>feval("fun",4)
Functions can be defined recursively! E.g. in fact.m:
function y = fact(n)
y = 1;
if n > 1
y = n*fact(n-1);
end
- Matrices. All variables in MATLAB are treated as matrices. Matrices can be entered directly:
>>A=[1 2 3; 4 5 6; 7 8 9]
- Matrices can be generated by other functions. Matrix Operations.
>>Z=zeros(3,5); %(a 3 x 5 matrix of zeroes)
>>X=ones(3,5); %(a 3 x 5 matrix of ones)
>>Y=0:0.5:2
>>cos(Y)
>>A(2,3)
>>A(1:2,2:3)
>>A([1 3],[1 3]) %(another submatrix)
>>A(2,2)=tan(7.8);
>>B=[1 2;3 4];
>>C=B'
>>C %(C is the transpose of B)
>>3*(B*C)^3 %3(BC)3
- Array Operations
>>A=[1 2; 3 4];
>>A^2 %(matrix power A2)
>>A.^2 %(squares each entry of A)
>>cos(A./2) %cos (aij/2)
For any matrix x, compare the difference between the results of 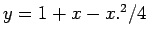 and
and 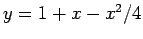
- Graphics
2- and 3-D plots of curves and surfaces. Use plot for 2-D functions.
For 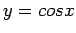 and
and 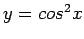 over
over ![$[0, \pi]$](img7.png) :
:
>>x=0:0.1:pi; %(step-size = 0.1)
>>y=cos(x);
>>z=cos(x).^2;
>>plot(x,y,x,z,'o') %(o's at (x_k, z_k))
fplot('name', [a,b],n) plots function name (in name.m) with n points (default 25) in [a, b].
>>fplot('tanh',[-2,2]) %(tanh x, x [-2, 2])
plot and plot3 for parametric curves in 2- and 3-D space.
Ex. Ellipse
![$c(t) = (2 cos t, 3 sin t), t \in [0, 2\pi]$](img8.png) :
:
>>t=0:0.2:2*pi;
>>plot(2*cos(t),3*sin(t))
Ex. Curve
![$c(t) = (2 cos t, t^2, 1/t), t \in [0.1, 4\pi]$](img9.png) :
:
>>t=0.1:0.1:4*pi;
>>plot3(2*cos(t),t.^2,1./t)
3-D surface plots, specify a rectangular subset of the domain of a function with meshgrid, mesh or surf.
>>x=-pi:0.1:pi;
>>y=x;
>>[x,y]=meshgrid(x,y);
>>z=sin(cos(x+y));
>>mesh(z)
- Loops and Conditionals
Relational Operators
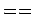 Equal to
Equal to
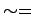 Not equal to
Not equal to
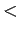 Less than
Less than
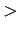 Greater than
Greater than
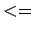 Less than or equal to
Less than or equal to
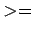 Greater than or equal to
Greater than or equal to
Logical Operators
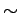 Not (complement)
Not (complement)
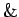 And (True if both operands true)
And (True if both operands true)
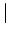 Or (True if either/both operands true)
Or (True if either/both operands true)
Boolean Values
1 True
0 false
Ex.
for i=1:5 %(Pascal's Triangle)
A(i,1)=1; A(1,i)=1;
end
for i=2:5
for j=2:5
A(i,j)=A(i,j-l)+A(i-l,j);
end
end
A
Ex.
for k=1:100
x=sqrt(k);
if ((k>10)&(x-floor(x)==0))
break
end
end
k
Ex.
n=10; k=0;
while k<=n
x=k/3;
disp([x x-2 x-3])
k=k+l;
end
- Programs: An effcient way to construct programs is to use user-defined functions, saved as m-files using the Editor/Debugger. These programs allow the user to specify the input and output parameters. They are easily called as subroutines in other programs. The following example mode out Pascal's triangle
with a prime number.
Ex.
function P=pasc(n,m)
%Input -- n is the number of rows
% -- m is the prime number
%Output -- P is Pascal's triangle
for j=l:n
P(j,1)=1; P(1,j)=1;
end
for k=2:n
for j=2:n
P(k,j)=rem(P(k,j-1),m)+rem(P(k-l,j),m);
end
end
for k=2:n
for j=2:n
P(k,j)=P(k,j-1)+P(k-l,j);
end
end
In the MATLAB Command Window, try
>>P=pasc(5,3)
to see the first five rows of Pascal's triangle mod 3. Or try
>>P=pasc(175,3); P
>>spy(P)
- Help
Information about specific MATLAB commands may obtained with the help command. Simply typing help by itself actually produces a listing of the available MATLAB "toolboxes" (groupings of related commands and functions), arranged by the general type of problem they are designed to solve, while typing help, followed by the name of a specific command. If you have any question about MATLAB commands, ask to MATLAB as
>>help
>>help general
>>help ops
>>help spy
>>help det
>>help sym/det.m
- Give the command help chop and examine the output. Next, give, in sequence, the commands
chop( 27.321592 , 5 )
chop( 27.321592 , 4 )
chop( 27.321592 , 3 )
Are the answers what you expected?
- Very little of MATLAB is actually written in C. Most MATLAB toolbox commands and functions are really just text files containing sequences of other MATLAB commands and functions. Such files are commonly called m-files, and are clearly identified because their Windows file name ends in .m. The commands and functions stored in an m-file are then executed whenever the user appropriately enters the corresponding file name. (Having commands and functions written in the more easily-readable MATLAB syntax, rather than in C, will significantly simplify our inspection and analysis of MATLAB algorithms.)
- As we have already briefly reviewed in this laboratory, and as we shall see even more clearly in the rest of this course, MATLAB provides powerful capabilites for theoretical and computational numerical analysis. However, one drawback of MATLAB is that, by and large, it can only perform numeric computation, i.e. every MATLAB command causes a number of floating point computations to be made and the resulting number(s) displayed. Another area of computation that is beginning to come into its own is symbolic computation, which involves the manipulation of algebraic expressions, and not just numbers. The difference between these two types of computation is that, for example, a numeric computation package will only be able to tell you that
while a symbolic computation program (i.e., Mathematica, MAPLE) will also tell you that