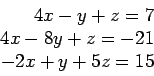Solving Sets of Equations

1. The following MATLAB codes is given for Upper Triangularization Followed by Back Substitution. To construct the solution to $Ax=b$, by first reducing the augmented matrix $[A\vert b]$ to upper-triangular form then performing back substitution.

   function X = uptrbk(A,B)
   %Input  - A is an N x N nonsingular matrix
   %       - B is an N x 1 matrix
   %Output - X is an N x 1 matrix containing the solution to AX=B.
   
   %Initialize X and the temporary storage matrix C 
   [N N]=size(A);
   X=zeros(N,1);
   C=zeros(1,N+1);
   
   %Form the augmented matrix: Aug=[A|B]
   Aug=[A B];
   
   for p=1:N-1
      %Partial pivoting for column p
      [Y,j]=max(abs(Aug(p:N,p)));
      %Interchange row p and j
      C=Aug(p,:);
      Aug(p,:)=Aug(j+p-1,:);
      Aug(j+p-1,:)=C;
     
      if Aug(p,p)==0
         'A was singular.  No unique solution'
        break
     end
     %Elimination process for column p
     for k=p+1:N
        m=Aug(k,p)/Aug(p,p);
        Aug(k,p:N+1)=Aug(k,p:N+1)-m*Aug(p,p:N+1);
     end
   end
   
   X=backsub(Aug(1:N,1:N),Aug(1:N,N+1));
   

   And for back substitution;

   function X=backsub(A,B)  
   %Input  - A is an n x n upper-triangular nonsingular matrix
   %	      - B is an n x 1 matrix
   %Output - X is the solution to the linear system AX = B
   
   %Find the dimension of B and initialize X
    n=length(B);
    X=zeros(n,1);
    X(n)=B(n)/A(n,n);
   
   for k=n-1:-1:1
    X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k);
   end
   

   • Analyze the MATLAB codes above, then by using solve the following linear system;
     
     $$\begin{array}{r} x_1+2x_2+x_3+4x_4=13\\ 2x_1+4x_3+3x_4=28... ... 4x_1+2x_2+2x_3+x_4=20\\ -3x_1+x_2+3x_3+2x_4=6\\ \end{array}$$
     
     
     • answer: $x=[3,-1,4,2]$
2. The following MATLAB code is given for $PA=LU$:Factorization with Pivoting. To construct the solution to $Ax=b$, where $A$ is a nonsingular matrix.

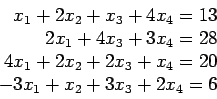
   function X = lufact(A,B)
   %Input  - A is an N x N matrix
   %	      - B is an N x 1 matrix
   %Output - X is an N x 1 matrix containing the solution to AX = B.
   
   %Initialize X, Y,the temporary storage matrix C, and the row 
   % permutation information matrix R
   
   [N,N]=size(A);
   X=zeros(N,1);
   Y=zeros(N,1);
   C=zeros(1,N);
   R=1:N;
   
   for p=1:N-1
      %Find the pivot row for column p
      [max1,j]=max(abs(A(p:N,p)));
      %Interchange row p and j
         C=A(p,:);
         A(p,:)=A(j+p-1,:);
         A(j+p-1,:)=C;
         d=R(p);
         R(p)=R(j+p-1);
         R(j+p-1)=d;
      if A(p,p)==0
         'A is singular.  No unique solution'
         break
      end
      %Calculate multiplier and place in subdiagonal portion of A
         for k=p+1:N
            mult=A(k,p)/A(p,p);
   	 A(k,p) = mult;
            A(k,p+1:N)=A(k,p+1:N)-mult*A(p,p+1:N);
         end
   end
   %Solve for Y
   Y(1) = B(R(1));
   for k=2:N
      Y(k)= B(R(k))-A(k,1:k-1)*Y(1:k-1);
   end
   %Solve for X
   X(N)=Y(N)/A(N,N);
   for k=N-1:-1:1
      X(k)=(Y(k)-A(k,k+1:N)*X(k+1:N))/A(k,k);
   end
   

   • Analyze the MATLAB code above, then by using solve the following linear system;
     
     $$\begin{array}{r} x_1+2x_2+4x_3+x_4=21\\ 2x_1+8x_2+6x_3+4x... ...+10x_2+8x_3+8x_4=79\\ 4x_1+12x_2+10x_3+6x_4=82\\ \end{array}$$
     
     
     • $Ax=b$
     • $LUAx=b$
     • defining $y=Ux$ then solving two systems:
     • first solve $Ly=b$ for $y$ by using forward-substitution method
     • then solve $Ux=y$ for $x$ by using back-substitution method
     • answers: $y=[21,10,6,-24]$ and $x=[1,2,3,4]$
3. The following MATLAB code is given for Jacobi Iteration. To solve the linear system $Ax=b$ by starting with an initial guess $x=P_0$ and generating a sequence ${P_k}$ that converges to the solution. A sufficient condition for the method to be applicable is that $A$ is strictly diagonally dominant.

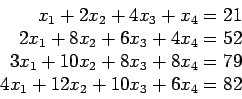
   function X=jacobi(A,B,P,delta, max1)
   % Input  - A is an N x N nonsingular matrix
   %        - B is an N x 1 matrix
   %        - P is an N x 1 matrix; the initial guess
   %	       - delta is the tolerance for P
   %	       - max1 is the maximum number of iterations
   % Output - X is an N x 1 matrix: the jacobi approximation to
   %	        the solution of AX = B
   
   N = length(B);
   for k=1:max1
      for j=1:N
         X(j)=(B(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j);
      end
      err=abs(norm(X'-P));
      relerr=err/(norm(X)+eps);
      P=X';
         if (err<delta)|(relerr<delta)
        break
      end
   end
   X=X';
   

   • Analyze the MATLAB code above, then by using solve the following linear system;
     
     $$\begin{array}{r} 4x-y+z=7\\ 4x-8y+z=-21\\ -2x+y+5z=15\\ \end{array}$$
     
     
     • Start by $P_0=(1,2,2)$; then answer: $x=2,y=4,z=3$ and number of iterations $k=19$.
     • Try some other starting sets and compare them.