- i
- What is the relationship that the graph suggests? Use least squares method to find out the necessary parameters of this suggested formula.
- ii
- Estimate the population at the years of 1995, 2007,2010 with least squares method.
- iii
- Fit a cubic (
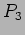 ) polynomial to the given data.
) polynomial to the given data.
- iv
- Estimate the population at the years of 1995, 2007,2010 with fitted polynomial.
- v
- Compare your results for both least squares and interpolated polynomial methods.
where
- vi
- Use this formula to approximate the derivative of
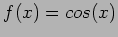 at
at  using step sizes of
using step sizes of 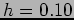 and
and 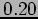 .
.
- vii
- Make an error analysis. Estimate the order of error
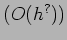 .
.
Hints: The ratio of errors and the difference with the exact value.
| 2.0 | 5.1 |
| 2.3 | 7.5 |
| 2.6 | 10.6 |
| 2.9 | 14.4 |
| 3.2 | 10.0 |
Hint: The two-term recursion formula
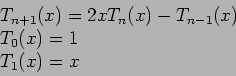
| 0.0000 | 0.0000 |
| 0.2000 | 0.5879 |
| 0.4000 | 1.0637 |
| 0.6000 | 1.3927 |
| 0.8000 | 1.5573 |
| 1.0000 | 1.5575 |
| 1.2000 | 1.4091 |
- viii
- Approximate
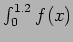 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 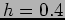 .
.
- ix
- Approximate
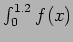 dx using the Trapezoidal Rule and a step size of
dx using the Trapezoidal Rule and a step size of 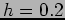 .
.
- x
- Estimate the error in your answer to previous item. Hint: Use the procedure to estimate the proportionality factor,
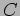 .
.
![\includegraphics[scale=1]{numerical/27afinal.ps}](img1.png)
![\includegraphics[scale=0.4]{numerical/27bfinal.ps}](img2.png)