Next: About this document ...

>> a=(-1*cos(0.4)+4*cos(0.2)-3*cos(0))/0.4 a = -0.0020
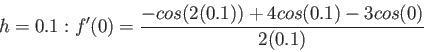
>> b=(-1*cos(0.2)+4*cos(0.1)-3*cos(0))/0.2 b = -2.4958e-04ii) The exact value is:
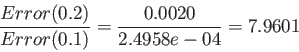
>> syms x; >> fx='sqrt(x)-cos(x)' fx = sqrt(x)-cos(x) >> subs(fx,0.0) ans = -1 >> subs(fx,1.0) ans = 0.45969769413186
| i | |
|
|
|
|
| 1 | 0.00000 | 1.00000 | 0.50000 | 0.12500 | 0.29370 |
| 2 | 0.50000 | 1.00000 | 0.75000 | 0.42188 | 0.04370 |
| 3 | 0.75000 | 1.00000 | 0.87500 | 0.66992 | 0.08130 |
| 4 | 0.75000 | 0.87500 | 0.81250 | 0.53638 | 0.01880 |
| 5 | 0.75000 | 0.81250 | 0.78125 | 0.47840 | 0.01245 |

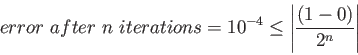
| i | |
|
|
|
|
| 1 | 0 | 1 | 0.5 | 0.12500 | 0.29370 |
| 2 | 0.5 | 1 | 0.75 | 0.42188 | 0.04370 |
| 3 | 0.75 | 1 | 0.875 | 0.66992 | 0.08130 |
| 4 | 0.75 | 0.875 | 0.8125 | 0.53638 | 0.01880 |
| 5 | 0.75 | 0.8125 | 0.78125 | 0.4784 | 0.01245 |
| 6 | 0.78125 | 0.8125 | 0.79688 | 0.50602 | 0.00318 |
| 7 | 0.78125 | 0.79688 | 0.789078 | 0.49130 | 0.00463 |
| 8 | 0.78907 | 0.79688 | 0.79298 | 0.49164 | 0.00072 |
| 9 | 0.79298 | 0.79688 | 0.79493 | 0.50233 | 0.00123 |
| 10 | 0.79298 | 0.79493 | 0.79396 | 0.50049 | 0.00026 |
| 11 | 0.79298 | 0.79396 | 0.79347 | 0.49956 | 0.00023 |
| 12 | 0.79347 | 0.79396 | 0.79372 | 0.50004 | 0.00002 |
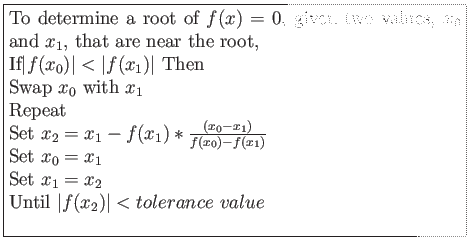
>> x0=1.0;
>> x1=0.0;
>> syms x;
fx='sqrt(x)-cos(x)';
>> subs(fx,x0)
ans = 0.45969769413186
>> subs(fx,x1)
ans = -1
>> x2=x1-subs(fx,x1)*((x0-x1)/(subs(fx,x0)-subs(fx,x1)))
x2 = 0.68507335732605
>> x0=x1
x0 = 0
>> x1=x2
x1 = 0.68507335732605
>> x2=x1-subs(fx,x1)*((x0-x1)/(subs(fx,x0)-subs(fx,x1)))
x2 = 0.65039498012836
>> solve('sqrt(x)-cos(x)')
ans = .64171437087288265839856530031652
![\begin{displaymath}
A=\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
2 & 5 & 2 & 2 \\
-1 &-3 &-3 & 5 \\
1 & 3 & 2 & 2 \\
\end{array} \right]
\end{displaymath}](img46.png)
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
2 & 5 & 2 & 2...
...\
0 & 0 & -2 & 6 \\
0 & 0 & 1 & 1 \\
\end{array} \right],
\end{displaymath}](img49.png)
![\begin{displaymath}
\begin{array}{r}
\\
\\
\\
R_4-(1/-2)R_3 \rightarrow \...
...\\
0 & 0 & -2 & 6 \\
0 & 0 & 0 & 4 \\
\end{array} \right]
\end{displaymath}](img50.png)
![\begin{displaymath}
U=\left[
\begin{array}{rrrr}
1 & 3 & 1 & 1 \\
0 & -1 & 0 ...
...
-1 & -3 & -3 & 5 \\
1 & 3 & 2 & 2 \\
\end{array} \right]
\end{displaymath}](img51.png)
>> L=[1 0 0 0 ; 2 1 0 0; -1 0 1 0; 1 0 -0.5 1]
L =
1.00000000000000 0 0 0
2.00000000000000 1.00000000000000 0 0
-1.00000000000000 0 1.00000000000000 0
1.00000000000000 0 -0.50000000000000 1.00000000000000
>> U=[1 3 1 1; 0 -1 0 0; 0 0 -2 6; 0 0 0 4]
U =
1 3 1 1
0 -1 0 0
0 0 -2 6
0 0 0 4
>> L*U
ans =
1 3 1 1
2 5 2 2
-1 -3 -3 5
1 3 2 2