Next: About this document ...
![\includegraphics[width=3cm]{numerical/CankayaLogo_yeni}](img1.png) |
Çankaya University
Mcs 331 Numerical Methods Final Examination Dec 31, 2014 09.30 - 11.30 Good Luck! |
![\includegraphics[width=3cm]{numerical/DepartmentLogo_yeni}](img2.png) |
|
|
![\begin{displaymath}
A=\left[
\begin{array}{rrr}
3 &-1 &2\\
1 & 1 &3\\
-3 & 0 &5\\
\end{array} \right]
\end{displaymath}](img4.png)
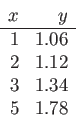
|
When a log-log plot of stress versus cycles is generated, the data trend shows a linear relationship;
|
![\begin{table}
% latex2html id marker 112
\begin{minipage}[h]{0.43\linewidth}
\ce...
...sion for this function up to $2^{nd}$\ term.
\end{list}\end{minipage}\end{table}](img14.png)
![\begin{table}\begin{minipage}[h]{0.43\linewidth}
\centering
\includegraphics[sca...
...te $Q$\ using the \textit{Composite Trapezoidal Rule}.
\end{minipage}\end{table}](img23.png)
|
|