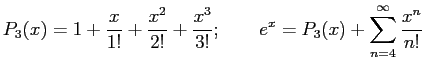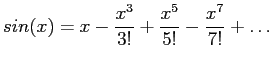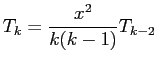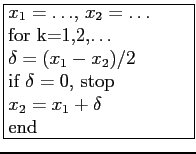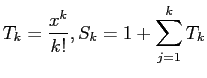Errors can occur in doing numerical procedures
>> format long e
>> 2.6+0.2
ans = 2.800000000000000e+00
>> ans+0.2
ans = 3.000000000000000e+00
>> ans+0.2
ans = 3.200000000000001e+00
Repeated addition of the perfectly reasonable fraction results in the creation of an erroneous digit.
>> 2.6+0.6
ans = 3.200000000000000e+00
>> ans+0.6
ans = 3.800000000000000e+00
>> ans+0.6
ans = 4.400000000000000e+00
>> ans+0.6
ans = 5
Not only is there no apparent loss of precision, but MATLAB displays the final results as 5, as integer. This behaviors are caused by the finite arithmetic used in numerical computations.
Computers use only a fixed number of digits to represent a number. As a result, the numerical values stored in a computer are said to have finite precision. Limiting precision has the desirable effects of increasing the speed of numerical calculations and reducing memory required to store numbers. What are the undesirable effects?
Kinds of Errors:
- Error in original Data
- Blunders: Sometimes a test run with known results is worthwhile, but is no guarantee of freedom from foolish error.
- Truncation Error: i.e., approximate
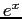 by the cubic power
by the cubic power
approximating 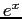 with the cubic gives an inexact answer. The error is due to truncating the series.
with the cubic gives an inexact answer. The error is due to truncating the series.
When to cut series expansion
 be satisfied with an approximation to the exact analytical answer.
be satisfied with an approximation to the exact analytical answer.
Unlike roundoff, which is controlled by the hardware and the computer language being used, truncation error is under control of the programmer or user. Truncation error can be reduced by selecting more accurate discrete approximations. It can not be eliminated entirely.
Example m-file: Evaluating the Series for sin(x) (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/sinser.m sinser.m)
An efficient implementation of the series uses recursion to avoid overflow in the evaluation of individual terms. If 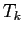 is the
is the 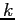 th term (
th term (
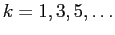 ) then
) then
>> sinser(pi/6)
Study the effect of the parameters tol and nmax by changing their values.
- Propagated Error:
- more subtle
- by propagated we mean an error in the succeeding steps of a process due to an Occurrence of an earlier error
- of critical importance
- stable numerical methods; errors made at early points die out as the method continues
- unstable numerical method; does not die out
- Round-off Error:
>> format long e %display all available digits
>> x=(4/3)*3
x = 4
>> a=4/3 %store double precision approx of 4/3
a = 1.333333333333333e+00
>> b=a-1 %remove most significant digit
b = 3.333333333333333e-01
>> c=1-3*b %3*b=1 in exact math
c = 2.220446049250313e-16 %should be 0!!
To see the effects of roundoff in a simple calculation, one need only to force the computer to store the intermediate results.
- All computing devices represents numbers, except for integers and some fractions, with some imprecision
- floating-point numbers of fixed word length; the true values are usually not expressed exactly by such representations
- if the number are rounded when stored as floating-point numbers, the round-off error is less than if the trailing digits were simply chopped off
- Absolute vs Relative Error:
>> x=tan(pi/6)
x = 5.773502691896257e-01
>> y=sin(pi/6)/cos(pi/6)
y = 5.773502691896256e-01
>> if x==y
fprintf('x and y are equal \n');
else
fprintf('x and y are not equal : x-y =%e \n',x-y);
end
x and y are not equal : x-y =1.110223e-16
The test is true only if 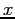 and
and 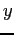 are exactly equal in bit pattern. Although
are exactly equal in bit pattern. Although 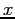 and
and 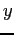 are equal in exact arithmetic, their values differ by a small, but nonzero, amount. When working with floating-point values the question "are
are equal in exact arithmetic, their values differ by a small, but nonzero, amount. When working with floating-point values the question "are 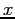 and
and 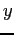 equal?" is replaced by "are
equal?" is replaced by "are 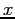 and
and 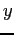 close?" or, equivalently, "is
close?" or, equivalently, "is 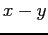 small enough?"
small enough?"
- accuracy (how close to the true value)
 great importance
great importance
-
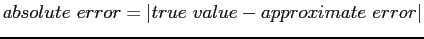
A given size of error is usually more serious when the magnitude of the true value is small
-
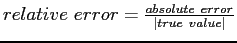
- Convergence of Iterative Sequences: Iteration is a common component of numerical algorithms. In the most abstract form, an iteration generates a sequence of scalar values
 . The sequence converges to a limit
. The sequence converges to a limit 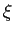 if
if
where 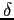 is a small number called the convergence tolerance. We say that the sequence has converged to within the tolerance
is a small number called the convergence tolerance. We say that the sequence has converged to within the tolerance 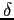 after
after 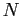 iterations.
iterations.
Example m-file: Iterative Computation of the Square Root (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/testSqrt.m testSqrt.m, http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/newtsqrtBlank.m newtsqrtBlank.m)
The goal of this example is to explore the use of different expressions to replace the "NOT_CONVERGED" string in the while statement. Some suggestions are given as:
r~=rold
(r-rold)> delta
abs(r-rold)>delta
abs((r-rold)/rold)>delta
Study each case, and which one should be used?
- Floating-Point Arithmetic: Performing an arithmetic operation
 no exact answers unless only integers or exact powers of 2 are involved
no exact answers unless only integers or exact powers of 2 are involved
- floating-point (real numbers)
 not integers
not integers
- resembles scientific notation
Table 2.1:
Floating
 Normalized.
Normalized.
| floating |
normalized (shifting the decimal point) |
| 13.524 |
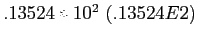 |
| -0.0442 |
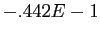 |
- IEEE standard
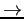 storing floating-point numbers (see the Table 2.1)
storing floating-point numbers (see the Table 2.1)
- the sign
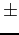
- the fraction part (called the mantissa)
- the exponent part
- There are three levels of precision (see the Fig. 2.3)
Figure 2.3:
Level of precision.
|
|
- Rather than use one of the bits for the sign of the exponent, exponents are biased. For single precision:
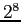 =256
=256
0
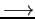 00000000 = 0
00000000 = 0
255
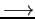 11111111=255
11111111=255
0 (255)
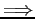 -127 (128). An exponent of -127 (128) stored as 0 (255).
-127 (128). An exponent of -127 (128) stored as 0 (255).
So biased
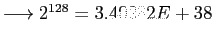 , mantissa gets 1 as maximum
, mantissa gets 1 as maximum
Largest: 3.40282E+38; Smallest: 2.93873E-39
For double and extended precision the bias values are 1023 and 16383, respectively.
- Certain mathematical operations are undefined,
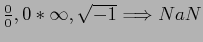
>> realmin
ans = 2.2251e-308
>> realmax
ans = 1.7977e+308
>> format long e
>> 10*realmax
ans = Inf
>> realmin
ans = 2.225073858507201e-308
>> realmin/10
ans = 2.225073858507203e-309
>> realmin/1e16
ans = 0
When a calculation results in a value smaller than realmin, there are two types of outcomes. If the result is slightly smaller than realmin, the number is stored as a denormal (they have fewer significant digits than normal floating point numbers). Otherwise, It is stored as 0.
Example m-file: Interval Halving to Oblivion (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/halfDiff.m halfDiff.m)
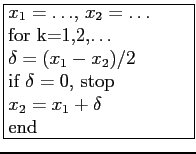
As the floating-point numbers become closer in value, the computation of their difference relies on digits with decreasing significance. When the difference is smaller than the least significant digit in their mantissa, the value of 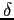 becomes zero.
becomes zero.
- EPS: short for epsilon
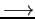 used for represent the smallest machine value that can be added to 1.0 that gives a result distinguishable from 1.0
In MATLAB:
used for represent the smallest machine value that can be added to 1.0 that gives a result distinguishable from 1.0
In MATLAB:
>> eps
ans=2.2204E-016
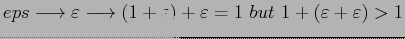
Two numbers that are very close together on the real number line can not be distinguished on the floating-point number line if their difference is less than the least significant bit of their mantissas.
- Round-off Error vs Truncation Error: Round-off occurs, even when the procedure is exact, due to the imperfect precision of the computer
Analytically
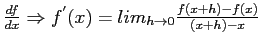 : procedure
: procedure
approximate value for 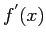 with a small value for h.
with a small value for h.
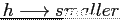 , the result is closer to the true value
, the result is closer to the true value
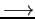 truncation error is reduced
truncation error is reduced
but at some point (depending of the precision of the computer) round-off errors will dominate
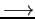 less exact
less exact
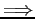 There is a point where the computational error is least.
There is a point where the computational error is least.
Example m-file: Roundoff and Truncation Errors in the Series for 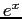 (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/expSeriesPlot.m expSeriesPlot.m)
(http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter0/expSeriesPlot.m expSeriesPlot.m)
Let 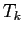 be the
be the 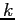 th term in the series and
th term in the series and 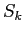 be the value of the sum after
be the value of the sum after 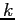 terms:
terms:
If the sum on the right-hand side is truncated after 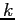 terms, the absolute error in the series approximation is
terms, the absolute error in the series approximation is
>> expSeriesPlot(-10,5e-12,60)
As 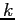 increases,
increases, 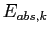 decreases, due to a decrease in the truncation error. Eventually, roundoff prevents any change in
decreases, due to a decrease in the truncation error. Eventually, roundoff prevents any change in 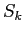 . As
. As
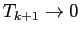 , the statement
, the statement
produces no change in 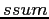 . For
. For  this occurs at
this occurs at 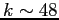 . At this point, the truncation error,
. At this point, the truncation error, 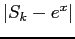 is not zero. Rather,
is not zero. Rather,
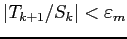 . This is an example of the independence of truncation error and roundoff error. For
. This is an example of the independence of truncation error and roundoff error. For 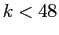 , the error in evaluating the series is controlled by truncation error. For
, the error in evaluating the series is controlled by truncation error. For 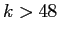 , roundoff error prevents any reduction in truncation error.
, roundoff error prevents any reduction in truncation error.
- Well-posed and well-conditioned problems: The accuracy depends not only on the computer's accuracy
- A problem is well-posed if a solution; exists, unique, depends on varying parameters
- A nonlinear problem
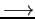 linear problem
linear problem
- infinite
 large but finite
large but finite
- complicated
 simplified
simplified
- A well-conditioned problem is not sensitive to changes in the values of the parameters (small changes to input do not cause to large changes in the output)
- Modelling and simulation; the model may be not a really good one
- if the problem is well-conditioned, the model still gives useful results in spite of small inaccuracies in the parameters
- Forward and Backward Error Analysis:
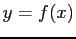
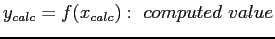
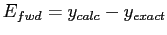 where
where 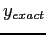 is the value we would get if the computational error were absent
is the value we would get if the computational error were absent
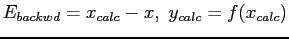
Example:
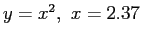 used only two digits
used only two digits
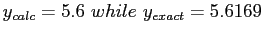
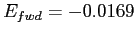 , relative error
, relative error
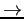 0.3
0.3
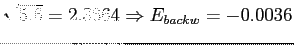 , relative error
, relative error
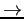 0.15
0.15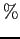
- Examples of Computer Numbers:
Say we have six bit representation (not single, double) (see the Fig. 2.4)
Figure 2.4:
Computer numbers with six bit representation.
|
|
For positive range

For negative range
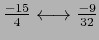 ; even discontinuity at point zero since it is not in the ranges.
; even discontinuity at point zero since it is not in the ranges.
Figure 2.5:
Upper: number line in the hypothetical system, Lower: IEEE standard.
|
|
Very simple computer arithmetic system
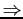 the gaps between stored values are very apparent. Many values can not be stored exactly. i.e., 0.601, it will be stored as if it were 0.6250 because it is closer to
the gaps between stored values are very apparent. Many values can not be stored exactly. i.e., 0.601, it will be stored as if it were 0.6250 because it is closer to
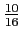 , an error of
, an error of 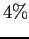 In IEEE system, gaps are much smaller but they are still present. (see the Fig. 2.5)
In IEEE system, gaps are much smaller but they are still present. (see the Fig. 2.5)
- Anomalies with Floating-Point Arithmetic:
For some combinations of values, these statements are not true
-
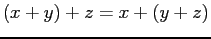
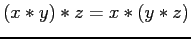
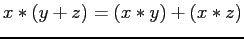
- adding 0.0001 one thousand times should equal 1.0 exactly but this is not true with single precision
-
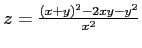 , problem with single precision
, problem with single precision
Cem Ozdogan
2011-12-27