Interval Halving (Bisection)
An algorithm for halving the interval (Bisection):
- Think about the multiplication factor, 2.
- The final value of
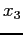 approximates the root, and it is in error by not more than
approximates the root, and it is in error by not more than
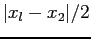 .
.
- The method may produce a false root if
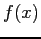 is discontinuous on
is discontinuous on ![$ [x_1,x_2]$](img232.png) .
.
>> format long e
>> fa=1e-120;fb=-2e-300;
>> fa*fb
ans = 0
>> sign(fa)~=sign(fb)
ans = 1
- Example: Apply Bisection to
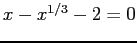 . http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/demoBisect.m m-file: demoBisect.m
. http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/demoBisect.m m-file: demoBisect.m
>> demoBisect(3,4)
- Example: Bracketing the roots of the function,
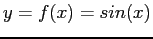 . http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/brackPlot.m m-file: brackPlot.m
. http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter1/brackPlot.m m-file: brackPlot.m
>> brackPlot('sin',-pi,pi)
>> brackPlot('sin',-2*pi,2*pi)
>> brackPlot('sin',-4*pi,4*pi)
- Now, try with a user (you!) defined function;
>> brackPlot('fx3',?,?)
In both example, try with different intervals.
- Example: The function;
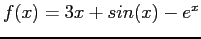
- Look at to the plot of the function to learn where the function crosses the x-axis. MATLAB can do it for us:
Figure 3.2:
Plot of the function:
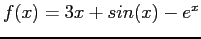
|
|
- We see from the figure that indicates there are zeros at about
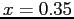 and
and 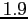 .
.
Table 3.1:
The bisection method for
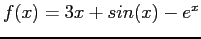 , starting from
, starting from
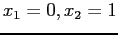 , using a tolerance value of 1E-4.
, using a tolerance value of 1E-4.
![\begin{table}
\begin{center}
\includegraphics[scale=0.6,angle=1.3]{figures/1-5}
\end{center}\end{table}](img240.png) |
- To obtain the true value for the root, which is needed to compute the actual error
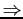 MATLAB
MATLAB
- A general implementation of bisection (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations//mfiles/chapter1/bisect.m m-file: bisect.m)
- It is shown above how brackPlot can be combined with bisect to find a single root of an equation.
- The same procedure can be extended to find more than one root if more than root exists. Consider the code
Use an appropriate 'myFunction', a suggestion is sine function.
The root is (almost) never known exactly, since it is extremely unlikely that a numerical procedure will find the precise value of 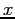 that makes
that makes 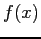 exactly zero in floating-point arithmetic.
exactly zero in floating-point arithmetic.
- The main advantage of interval halving is that it is guaranteed to work (continuous & bracket).
- The algorithm must decide how close to the root the guess should be before stopping the search (see Fig. 3.3).
Figure 3.3:
The stopping criterion for a root-finding procedure should involve a tolerance on 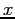 , as well as a tolerance on
, as well as a tolerance on 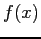 .
.
|
|
- This guarantee can be avoided, if the function has a slope very near to zero at the root.
- Because the interval
![$ [a, b]$](img245.png) is halved each time, the number of iterations to achieve a specified accuracy is known in advance.
is halved each time, the number of iterations to achieve a specified accuracy is known in advance.
- The last value of
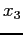 differs from the true root by less than
differs from the true root by less than
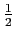 the last interval.
the last interval.
- So we can say with surely that
- When there are multiple roots, interval halving may not be applicable, because the function may not change sign at points on either side of the roots.
- The major objection of interval halving has been that it is slow to converge.
- Bisection is generally recommended for finding an approximate value for the root, and then this value is refined by more efficient methods.
Cem Ozdogan
2011-12-27

![]() that makes
that makes ![]() exactly zero in floating-point arithmetic.
exactly zero in floating-point arithmetic.
