- Another rearrangement of
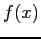 ; Let us start the iterations again with
; Let us start the iterations again with 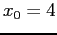 . Successive values then are:
. Successive values then are:
- It seems that we now converge to the other root, at
 .
.
- Consider a third rearrangement; starting again with
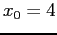 , we get
, we get
- The iterations are obviously diverging.
- The fixed point of
 is the intersection of the line
is the intersection of the line 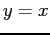 and the curve
and the curve 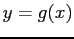 plotted against
plotted against  .
.
Figure 3.11:
The fixed point of  is the intersection of the line
is the intersection of the line 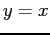 and the curve
and the curve 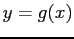 plotted against
plotted against 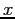 . Where A:
. Where A:
 . B:
. B:
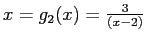 . C:
. C:
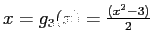 .
.
|
|
Figure 3.11 shows the three cases.
- Start on the x-axis at the initial
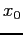 , go vertically to the curve, then horizontally to the line
, go vertically to the curve, then horizontally to the line 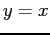 , then vertically to the curve, and again horizontally to the line.
, then vertically to the curve, and again horizontally to the line.
- Repeat this process until the points on the curve converge to a fixed point or else diverge.
- The method may converge to a root different from
the expected one, or it may diverge.
- Different rearrangements will converge at different rates.
- Iteration algorithm with the form

Cem Ozdogan
2011-12-27
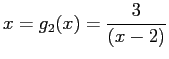
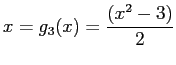
![\includegraphics[scale=0.37]{figures/1-23}](img328.png)
