Divided Differences

• There are two disadvantages to using the Lagrangian polynomial or Neville's method for interpolation.
  1. It involves more arithmetic operations than does the divided- difference method.
  2. More importantly, if we desire to add or subtract a point from the set used to construct the polynomial, we essentially have to start over in the computations.
• Both the Lagrangian polynomials and Neville's method also must repeat all of the arithmetic if we must interpolate at a new $x$-value.
• The divided-difference method avoids all of this computation.
• Actually, we will not get a polynomial different from that obtained by Lagrange's technique.

• Every $n^{th}$-degree polynomial that passes through the same $n + 1$ points is identical.
• Only the way that the polynomial is expressed is different.
• The function, $f(x)$, is known at several values for $x$:
  $$\begin{array}{rr} x_0 & f_0 \\ x_1 & f_1 \\ x_2 & f_2 \\ x_3 & f_3 \\ \end{array}$$

• We do not assume that the $x$'s are evenly spaced or even that the values are arranged in any particular order.
• Consider the $n^{th}$-degree polynomial written as:
  $$P_n(x) = a_0 + (x - x_0)a_1 + (x - x_0)(x - x_1)a_2 + (x - x_0)(x - x_1) \ldots (x - x_{n-1})a_n$$

• If we chose the $a_i$'s so that $P_n(x)= f(x)$ at the $n + 1$ known points, then $P_n(x)$ is an interpolating polynomial.

• The $a_i$'s are readily determined by using what are called the divided differences of the tabulated values.
• A special standard notation for divided differences is
  $$f[x_0,x_1]=\frac{f_1-f_0}{x_1-x_0}$$
  called the first divided difference between $x_0$ and $x_1$.
• And, $f[x_0]= f_0 = f(x_0)$ (zero-order difference).
  $$f[x_s]=f_s$$

• In general,
  $$f[x_s,x_t]=\frac{f_t-f_s}{x_t-x_s}$$

• Second- and higher-order differences are defined in terms of lower-order differences.
  $$f[x_0,x_1,x_2]=\frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}$$

• For n-terms,
  $$f[x_0,x_1,\ldots,x_n]=\frac{f[x_1,x_2,\ldots,f_n]-f[x_0,x_1,\ldots,f_{n-1}]}{x_n-x_0}$$

• Using the standard notation, a divided-difference table is shown in symbolic form in Table 5.3.
  

  Table 5.3: Divided-difference table in symbolic form.

  $x_i$	$f_i$	$f[x_i,x_{i+1}]$	$f[x_i,x_{i+1},x_{i+2}]$	$f[x_i,x_{i+1},x_{i+2},x_{i+3}]$
  $x_0$	$f_0$	$f[x_0,x_1]$	$f[x_0,x_1,x_2]$	$f[x_0,x_1,x_2,x_3]$
  $x_1$	$f_1$	$f[x_1,x_2]$	$f[x_1,x_2,x_3]$	$f[x_1,x_2,x_3,x_4]$
  $x_2$	$f_2$	$f[x_2,x_3]$	$f[x_2,x_3,x_4]$
  $x_3$	$f_3$	$f[x_3,x_4]$

  
  

Table 5.4: Divided-difference table in numerical values.

$x_i$	$f_i$	$f[x_i,x_{i+1}]$	$f[x_i,x_{i+1},x_{i+2}]$	$f[x_i,\ldots,x_{i+3}]$	$f[x_i,\ldots,x_{i+4}]$
3.2	22.0	8.400	2.856	-0.528	0.256
2.7	17.8	2.118	2.012	0.0865
1.0	14.2	6.342	2.263
4.8	38.3	16.750
5.6	51.7

• Table 5.4 shows specific numerical values.
  $$f[x_0,x_1]=\frac{f_1-f_0}{x_1-x_0}=\frac{17.8-22.0}{2.7-3.2}=8.4$$
  $$f[x_1,x_2]=\frac{f_2-f_1}{x_2-x_1}=\frac{14.2-17.8}{1.0-2.7}=2.1176$$
  $$f[x_0,x_1,x_2]=\frac{f[x_1,x_2]-f[x_0,x_1]}{x_2-x_0}=\frac{2.1176-8.4}{1.0-3.2}=2.8556$$
  and the others..
  

$$\begin{array}{ll} x=x_0: & P_0(x_0)=a_0 \\ x=x_1: & P_1(x_1... ..._2+\ldots\\ & +(x_n-x_0)\ldots(x_n-x_{n-1})a_n\\ \end{array}$$

• If $P_n(x)$ is to be an interpolating polynomial, it must match the table for all $n + 1$ entries:
  $$P_n(x_i)=f_i for i=0,1,2,\ldots,n.$$

• Each $P_n(x_i)$ will equal $f_i$, if $a_i=f[x_0,x_1,\ldots,x_i]$. We then can write:
  $$P_n(x)=f[x_0]+(x-x_0)f[x_0,x_1]+(x-x_0)(x-x_1)f[x_0,x_1,x_2]$$
  $$+(x-x_0)(x-x_1)(x-x_2)f[x_0,\ldots,x_3]$$
  $$+(x-x_0)(x-x_1)\ldots(x-x_{n-1})f[x_0,\ldots,x_n]$$

• Write interpolating polynomial of degree-3 that fits the data of Table 5.4 at all points $x_0=3.2$ to $x_3=4.8$.
  $$P_3(x)=22.0+8.400(x-3.2)+2.856(x-3.2)(x-2.7)$$
  $$-0.528(x-3.2)(x-2.7)(x-1.0)$$

• What is the fourth-degree polynomial that fits at all five points?
• We only have to add one more term to $P_3(x)$
  $$P_4(x)=P_3(x)+0.2568(x-3.2)(x-2.7)(x-1.0)(x-4.8)$$

• If we compute the interpolated value at $x=3.0$, we get the same result: $P_3(3.0)= 20.2120$.
• This is not surprising, because all third-degree polynomials that pass through the same four points are identical.
• They may look different but they can all be reduced to the same form.

• Example m-file: Constructs a table of divided-difference coefficients. Diagonal entries are coefficients of the polynomial. (http://siber.cankaya.edu.tr/ozdogan/NumericalComputations/mfiles/chapter3/divDiffTable.mdivDiffTable.m)

  

• Divided differences for a polynomial
• It is of interest to look at the divided differences for $f(x)=P_n(x)$.
• Suppose that $f(x)$ is the cubic
  $$f(x)=2x^3 - x^2 + x - 1.$$

• Here is its divided-difference table:
  

  $x_i$	$f[x_i]$	$f[x_i,x_{i+1}]$	$f[x_i,x_{i+1}$	$f[x_i,\ldots$	$f[x_i,\ldots$	$f[x_i,\ldots$
  			$,x_{i+2}]$	$,x_{i+3}]$	$,x_{i+4}]$	$,x_{i+5}]$
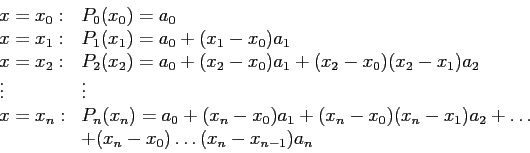
  0.30	-0.736	2.480	3.000	2.000	0.000	0.000
  1.00	1.000	3.680	3.600	2.000	0.000
  0.70	-0.104	2.240	5.400	2.000
  0.60	-0.328	8.720	8.200
  1.90	11.008	21.020
  2.10	15.212

• Observe that the third divided differences are all the same.
• It then follows that all higher divided differences will be zero.

$$P_3(x)=f[x_0]+(x-x_0)f[x_0,x_1]+(x-x_0)(x-x_1)f[x_0,x_1,x_2]$$

$$+(x-x_0)(x-x_1)(x-x_2)f[x_0,x_1,x_2,x_3]$$

which is same with the starting polynomial.