Ill-Conditioned Systems

• A system whose coefficient matrix is singular has no unique solution.
• What if the matrix is almost singular?
  
  $$A=\left[ \begin{array}{rrr} 3.02 & -1.05 & 2.53 \\ 4.33 & 0.56 &-1.78 \\ -0.83 &-0.54 & 1.47\\ \end{array} \right]$$
  
  

• The LU equivalent has a very small element in (3, 3),
  
  $$LU=\left[ \begin{array}{rrr} 4.33 & 0.56 &-1.78 \\ (0.697... ...15 \\ (-0.1917) & (0.3003) & -0.0039\\ \end{array} \right],$$
  
  

• Inverse has elements very large in comparison to $A$:
  
  $$inv(A)=\left[ \begin{array}{rrr} 5.6611 & -7.2732 &-18.5503... ...43 \\ 76.8511 & -102.6500 & -255.8846\\ \end{array} \right]$$
  
  

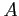• Matrix is nonsingular but is almost singular.

• Suppose we solve the system 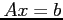$Ax=b$, with 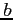$b$ equal to $[-1.61, 7.23, -3.38]^T$.
  • The solution is $x = [1.0000, 2.0000, -1.0000]^T$.
• Now suppose that we make a small change in just the first element of the 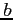$b$-vector : $[-1.60, 7.23, -3.38]^T$.
  • We get $x =[ 1.0566, 4.0051, -0.2315]^T$
• if $b=[-1.61, 7.22, -3.38]^T$, the solution now is $x = [1.07271, 4.6826, 0.0265]^T$ which also differs.

• A system whose coefficient matrix is nearly singular is called ill-conditioned.
• When a system is ill-conditioned, the solution is very sensitive
  • to small changes in the right-hand vector,
  • to small changes in the coefficients.
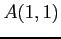• $A(1 , 1)$ is changed from 3.02 to 3.00, original b-vector, a large change in the solution $x =[1.1277, 6.5221, 0.7333]^T]$.
• This means that it is also very sensitive to round-off error.