Interpolation and Curve Fitting
- Sines, logarithms, and other nonalgebraic functions from tables
- Those tables had values of the function at uniformly spaced values of the argument.
- Most often interpolated linearly: The value for
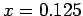 was computed as at the halfway point between
was computed as at the halfway point between 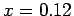 and
and 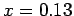 .
.
- If the function does not vary too rapidly and the tabulated points are close enough together, this linearly estimated value would be accurate enough.
- Data can be interpolated to estimate values
- Interpolating Polynomials: Describes a straightforward but computationally awkward way to fit a polynomial to a set of data points so that an interpolated value can be computed. The cost of getting the interpolant with a desired accuracy is facilitated by a variant, Neville's method.
- Divided Differences: These provide a more efficient way to construct an interpolating polynomial, one that allows one to readily change the degree of the polynomial. If the data are at evenly spaced x-values, there is some simplification.
- Spline Curves: Using special polynomials, splines, one can fit polynomials to data more accurately than with an interpolating polynomial. At the expense of added computational effort, some important problems that one has with interpolating polynomials is overcome.
- Least-Squares Approximations: Are methods by which polynomials and other functions can be fitted to data that are subject to errors likely in experiments. These approximations are widely used to analyze experimental observations.
Subsections
2004-12-28