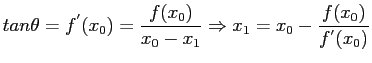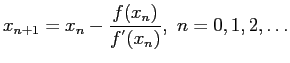Newton's Method

Figure 3.6: Graphical illustration of the Newton's Method.

One of the most widely used methods of solving equations is Newton's method (Newton did not publish an extensive discussion of this method, but he solved a cubic polynomial in Principia (1687)).

• The version given here is considerably improved over his original example.
• Like the previous ones, this method is also based on a linear approximation of the function, but does so using a tangent to the curve (see Figure 3.6).

• Starting from a single initial estimate, 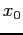$x_0$, that is not too far from a root, we move along the tangent to its intersection with the x-axis, and take that as the next approximation.
• This is continued until either the successive x-values are sufficiently close or the value of the function is sufficiently near zero.
• The calculation scheme follows immediately from the right triangle shown in Fig. 3.6.
  $$tan\theta=f^{'}(x_0)=\frac{f(x_0)}{x_0-x_1}\Rightarrow x_1=x_0-\frac{f(x_0)}{f^{'}(x_0)}$$
  and the general term is:
  $$x_{n+1}=x_{n}-\frac{f(x_n)}{f^{'}(x_n)}, n=0,1,2,\ldots$$