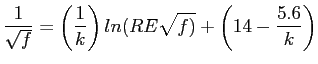- Interval Halving (Bisection). Describes a method that is very simple and foolproof but is not very efficient. We examine how the error decreases as the method continues.
- Linear Interpolation Methods. Tells how approximating the function in the vicinity of the root with a straight line can find a root more efficiently. It has a better "rate of convergence".
- 3
- Newton's Method. Explains a still more efficient method that is very widely used but there are pitfalls that you should know about. Complex roots can be found if complex arithmetic is employed.
- 4
- Muller's Method. Approximates the function with a quadratic
polynomial that fits to the function better than a straight line. This significantly improves the rate of convergence over linear interpolation.
- 5
- Fixed-Point Iteration:
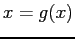 Method. Uses a different approach: The function
Method. Uses a different approach: The function 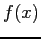 is rearranged to an equivalent form,
is rearranged to an equivalent form, 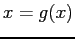 . A starting value,
. A starting value, 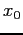 , is substituted into
, is substituted into 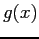 to give a new x-value,
to give a new x-value, 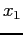 . This in turn is used to get another x-value. If the function
. This in turn is used to get another x-value. If the function 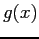 is properly chosen, the successive values converge.
is properly chosen, the successive values converge.
Subsections
Cem Ozdogan
2011-12-27