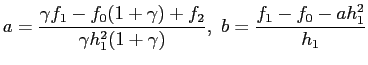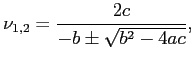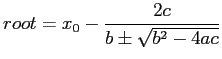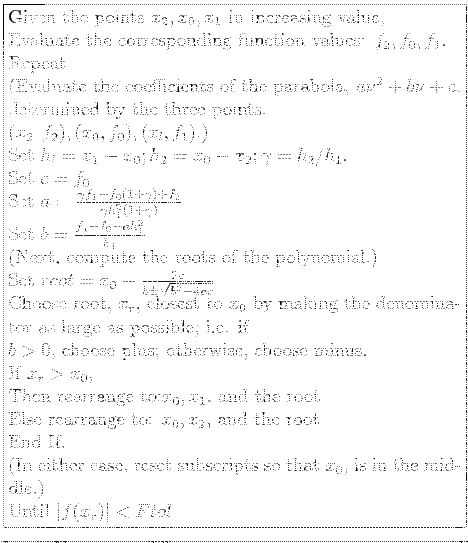- Most of the root-finding methods that we have considered so far have approximated the function in the neighbourhood of the root by a straight line.
- Muller's method is based on approximating the function in the neighbourhood of the root by a quadratic polynomial.
Figure 3.8:
Parabola
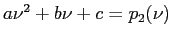
|
|
- A second-degree polynomial is made to fit three points near a root, at
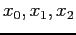 with
with 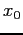 between
between 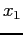 , and
, and 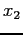 .
.
- The proper zero of this quadratic, using the quadratic formula, is used as the improved estimate of the root.
- A quadratic equation that fits through three points in the vicinity of a root, in the form
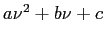 . (See Fig. 3.8)
. (See Fig. 3.8)
See Figs. 3.9-3.10 that an example is given
Figure 3.9:
An example of the use of Muller's method.
|
|
Figure 3.10:
Cont. An example of the use of Muller's method.
|
|
- Experience shows that Muller's method converges at a rate that is similar to that for Newton's method.
- It does not require the evaluation of derivatives, however, and (after we have obtained the starting values) needs only one function evaluation per iteration.
An algorithm for Muller's method :
Cem Ozdogan
2011-12-27
![]() at the three points:
at the three points: