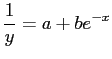Nonlinear Data, Curve Fitting
- In many cases, data from experimental tests are not linear,
- so we need to fit to them some function other than a first-degree polynomial.
- Popular forms are the exponential form
or
- We can develop normal equations to the preceding development for a least-squares line by setting the partial derivatives equal to zero.
- Such nonlinear simultaneous equations are much more difficult to solve than linear equations.
- Thus, the exponential forms are usually linearized by taking logarithms before determining the parameters,
For the case 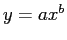
For the case
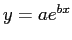
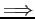
- We now fit the new variable,
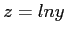 , as a linear function of
, as a linear function of 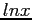 or
or 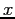 as described earlier (normal equations).
as described earlier (normal equations).
- Here we do not minimize the sum of squares of the deviations of
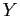 from the curve, but rather the deviations of
from the curve, but rather the deviations of 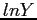 .
.
- In effect, this amounts to minimizing the squares of the percentage errors, which itself may be a desirable feature.
- An added advantage of the linearized forms is that plots of the data on either log-log or semilog graph paper show at a glance whether these forms are suitable, by whether a straight line represents the data when so plotted.
- In cases when such linearization of the function is not desirable,
- or when no method of linearization can be discovered, graphical methods are frequently used;
- one plots the experimental values and sketches in a curve that seems to fit well.
- Transformation of the variables to give near linearity,
- such as by plotting against
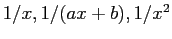 ,
,
- and other polynomial forms of the argument may give curves with gentle enough changes in slope to allow a smooth curve to be drawn.
- S-shaped curves are not easy to linearize; the relation
is sometimes employed.
- The constants
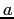 ,
, 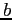 , and
, and 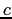 are determined by special procedures.
are determined by special procedures.
- Another relation that fits data to an S-shaped curve is
Cem Ozdogan
2011-12-27
![]()
![]()
![]()
![]()