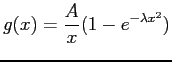Next: Use of Orthogonal Polynomials Up: Hands-on-Interpolation and Curve Fitting Previous: Nonlinear Data, Curve Fitting Contents
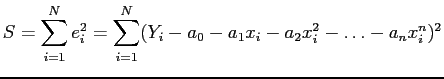
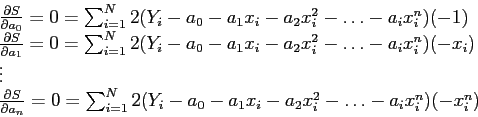
![\begin{displaymath}
A=\left[
\begin{array}{rrrrr}
1 & 1 & 1 & 1 & 1 \\
x_1 & ...
... x_1^n & x_2^n & x_3^n & \ldots & x_N^n\\
\end{array} \right]
\end{displaymath}](img847.png)
![\begin{displaymath}\overbrace{\left[
\begin{array}{rrrrr}
1 & 1 & 1 & 1 & 1 ...
... x_i^2Y_i\\
\vdots \\
\sum x_i^n Y_i\\
\end{array} \right]\end{displaymath}](img850.png) |
(5.8) |
![\begin{displaymath}
\overbrace{\left[
\begin{array}{rrrrr}
1 & 1 & 1 & \ldots &...
...^n & x_2^n & x_3^n & \ldots & x_N^n\\
\end{array} \right]}^A*
\end{displaymath}](img854.png)
![\begin{displaymath}
\overbrace{\left[
\begin{array}{rrrrr}
1 & x_1 & x_1^2 & \l...
...& x_N & x_N^2 & \ldots & x_N^n \\
\end{array} \right]}^{A^T}=
\end{displaymath}](img855.png)
![\begin{displaymath}
\underbrace{\left[
\begin{array}{rrrrrl}
N & \sum x_i & \sum...
... x_i^{n+3} & \ldots & \sum x_i^{2n}\\
\end{array} \right]}_B
\end{displaymath}](img856.png)
![\begin{displaymath}
\overbrace{\left[
\begin{array}{rrrrr}
1 & x_1 & x_1^2 & \l...
...& x_N & x_N^2 & \ldots & x_N^n \\
\end{array} \right]}^{A^T}*
\end{displaymath}](img858.png)
![\begin{displaymath}
\overbrace{\left[
\begin{array}{r}
a_0\\
a_1\\
a_2\\
\ldots\\
a_n\\
\end{array} \right]}^{a}=
\end{displaymath}](img859.png)
![\begin{displaymath}
\overbrace{\left[
\begin{array}{r}
y_1\\
y_2\\
y_3\\
\ldots\\
y_N\\
\end{array} \right]}^{y}
\end{displaymath}](img860.png)
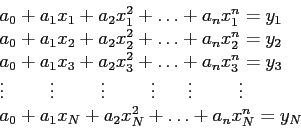
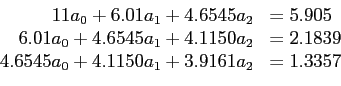
R/C: 0.73, 0.78, 0.81, 0.86, 0.875, 0.89, 0.95, 1.02, 1.03, 1.055, 1.135, 1.14, 1.245, 1.32, 1.385, 1.43, 1.445, 1.535, 1.57, 1.63, 1.755.
![]() : 0.0788, 0.0788, 0.064, 0.0788, 0.0681, 0.0703, 0.0703, 0.0681, 0.0681, 0.079, 0.0575, 0.0681, 0.0575, 0.0511, 0.0575, 0.049, 0.0532, 0.0511, 0.049, 0.0532,0.0426.
: 0.0788, 0.0788, 0.064, 0.0788, 0.0681, 0.0703, 0.0703, 0.0681, 0.0681, 0.079, 0.0575, 0.0681, 0.0575, 0.0511, 0.0575, 0.049, 0.0532, 0.0511, 0.049, 0.0532,0.0426.