- We have mentioned that the system of normal equations for a polynomial fit is ill-conditioned when the degree is high.
- Even for a cubic least-squares polynomial, the condition number of the coefficient matrix can be large.
- In one experiment, a cubic polynomial was fitted to 21 data points.
- When the data were put into the coefficient matrix of Eq. 5.7, its condition number (using 2-norms) was found to be 22000!.
- This means that small differences in the
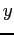 -values will make a large difference in the solution.
-values will make a large difference in the solution.
- In fact, if the four right-hand-side values are each changed by only 0.01 (about 0.1%),
- the solution for the parameters of the cubic were changed significantly, by as much as 44%!
- However, if we fit the data with orthogonal polynomials such as the Chebyshev polynomials.
- A sequence of polynomials is said to be orthogonal with respect to the interval [a,b], if
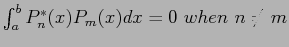 .
.
- The condition number of the coefficient matrix is reduced to about 5 and the solution is not much affected by the perturbations.
Cem Ozdogan
2011-12-27