Next: Boundary Value Problems Up: Initial Value Problems Previous: Runge-Kutta Method Contents
 and
and  :
:
 |
 |
 order equation, two 1
order equation, two 1 order equations are formed:
order equations are formed:
 |
 |
 |
|
 |
 |
 |
 a system with M first-order equations.
a system with M first-order equations.
 t order differential equation to these linear system.
t order differential equation to these linear system.
 |
 |
 |
|
 |
 |
 |
|
|
|
 degree system is written as:
degree system is written as:
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
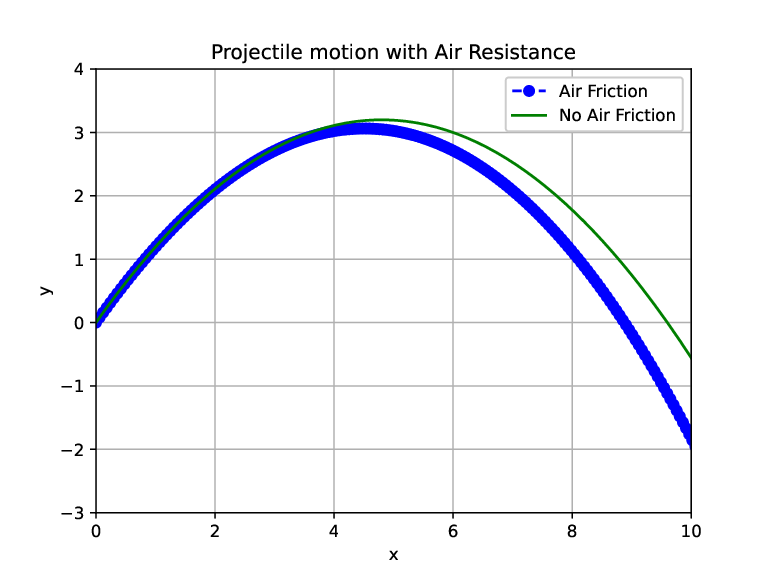
 in this system of equations, we obtain our usual parabolic curve
in this system of equations, we obtain our usual parabolic curve
 .
.
 ) and constants (
) and constants ( &
&  ):
):
 |
 |
||
 |
 |
||
 |
 |
|
 |
 |
 |
|
 |
 |
 |
|
|
|
 degree system is written as:
degree system is written as:
 |
 |
 |
|
 |
 |
 |
|
 |
 |
![$\displaystyle -\frac{GM}{[y_1^2+y_2^2]^{3/2}}y_1$](img301.svg) |
(5.3) |
 |
 |
![$\displaystyle -\frac{GM}{[y_1^2+y_2^2]^{3/2}}y_2$](img302.svg) |
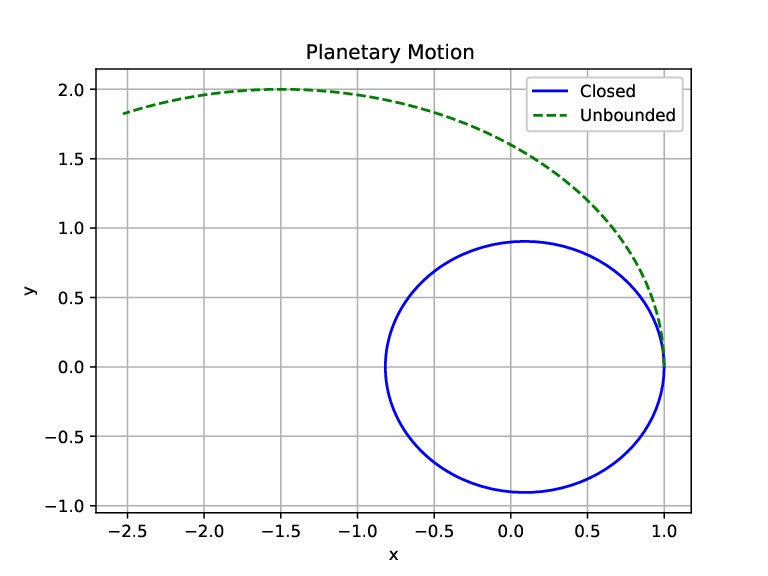
 . The time taken for the Earth to go around the Sun once is 1 year (y) as the unit of time.
. The time taken for the Earth to go around the Sun once is 1 year (y) as the unit of time.
 ,
,

 |
 |
||
 |
 |
 .
.
|