



Next: Two-Dimensional Matrix-Vector Multiplication
Up: Introduction to Parallel Algorithms
Previous: Cannon's Matrix-Matrix Multiplication with
Contents
One-Dimensional Matrix-Vector Multiplication
- The following http://siber.cankaya.edu.tr/ParallelComputing/cfiles/odrwmvm.c code segment is for multiplying a dense
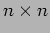 matrix
matrix  with a vector
with a vector 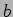 , i.e.,
, i.e., 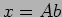 .
.
- One way of performing this multiplication in parallel is to have each process compute different portions of the product-vector
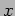 . In particular, each one of the
. In particular, each one of the 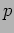 processes is responsible for computing
processes is responsible for computing 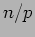 consecutive elements of
consecutive elements of 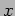 .
.
- This algorithm can be implemented in MPI by distributing the matrix
 in a row-wise fashion, such that each process receives the
in a row-wise fashion, such that each process receives the 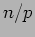 rows that correspond to the portion of the product-vector
rows that correspond to the portion of the product-vector 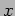 it computes. Vector
it computes. Vector 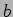 is distributed in a fashion similar to
is distributed in a fashion similar to 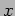 .
.
- Code segment shows the MPI program that uses a row-wise distribution of matrix
 . The dimension of the matrices is supplied in the parameter
. The dimension of the matrices is supplied in the parameter 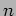 , the parameters
, the parameters  and
and 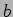 point to the locally stored portions of matrix
point to the locally stored portions of matrix  and vector
and vector 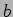 , respectively, and the parameter
, respectively, and the parameter 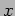 points to the local portion of the output matrix-vector product. This program assumes that
points to the local portion of the output matrix-vector product. This program assumes that 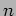 is a multiple of the number of processors.
is a multiple of the number of processors.
1 RowMatrixVectorMultiply(int n, double *a, double *b, double *x,
2 MPI_Comm comm)
3 {
4 int i, j;
5 int nlocal; /* Number of locally stored rows of A */
6 double *fb; /* Will point to a buffer that stores the entire vector b */
7 int npes, myrank;
8 MPI_Status status;
9
10 /* Get information about the communicator */
11 MPI_Comm_size(comm, &npes);
12 MPI_Comm_rank(comm, &myrank);
13
14 /* Allocate the memory that will store the entire vector b */
15 fb = (double *)malloc(n*sizeof(double));
16
17 nlocal = n/npes;
18
19 /* Gather the entire vector b on each processor using MPI's ALLGATHER operation */
20 MPI_Allgather(b, nlocal, MPI_DOUBLE, fb, nlocal, MPI_DOUBLE,
21 comm);
22
23 /* Perform the matrix-vector multiplication involving the locally stored submatrix */
24 for (i=0; i<nlocal; i++) {
25 x[i] = 0.0;
26 for (j=0; j<n; j++)
27 x[i] += a[i*n+j]*fb[j];
28 }
29
30 free(fb);
31 }
- An alternate way of computing
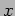 is to parallelize the task of performing the dot-product for each element of
is to parallelize the task of performing the dot-product for each element of 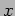 . That is, for each element
. That is, for each element 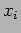 , of vector
, of vector 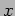 , all the processes will compute a part of it, and the result will be obtained by adding up these partial dot-products.
, all the processes will compute a part of it, and the result will be obtained by adding up these partial dot-products.
- This algorithm can be implemented in MPI by distributing matrix
 in a column-wise fashion. Each process gets
in a column-wise fashion. Each process gets 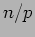 consecutive columns of
consecutive columns of  , and the elements of vector
, and the elements of vector 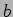 that correspond to these columns.
that correspond to these columns.
- Furthermore, at the end of the computation we want the product-vector
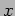 to be distributed in a fashion similar to vector
to be distributed in a fashion similar to vector 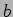 . The following http://siber.cankaya.edu.tr/ParallelComputing/cfiles/odcwmvm.c code segment shows the MPI program that implements this column-wise distribution of the matrix.
. The following http://siber.cankaya.edu.tr/ParallelComputing/cfiles/odcwmvm.c code segment shows the MPI program that implements this column-wise distribution of the matrix.
1 ColMatrixVectorMultiply(int n, double *a, double *b, double *x,
2 MPI_Comm comm)
3 {
4 int i, j;
5 int nlocal;
6 double *px;
7 double *fx;
8 int npes, myrank;
9 MPI_Status status;
10
11 /* Get identity and size information from the communicator */
12 MPI_Comm_size(comm, &npes);
13 MPI_Comm_rank(comm, &myrank);
14
15 nlocal = n/npes;
16
17 /* Allocate memory for arrays storing intermediate results. */
18 px = (double *)malloc(n*sizeof(double));
19 fx = (double *)malloc(n*sizeof(double));
20
21 /* Compute the partial-dot products that correspond to the local columns of A.*/
22 for (i=0; i<n; i++) {
23 px[i] = 0.0;
24 for (j=0; j<nlocal; j++)
25 px[i] += a[i*nlocal+j]*b[j];
26 }
27
28 /* Sum-up the results by performing an element-wise reduction operation */
29 MPI_Reduce(px, fx, n, MPI_DOUBLE, MPI_SUM, 0, comm);
30
31 /* Redistribute fx in a fashion similar to that of vector b */
32 MPI_Scatter(fx, nlocal, MPI_DOUBLE, x, nlocal, MPI_DOUBLE, 0,
33 comm);
34
35 free(px); free(fx);
36 }
- Comparing these two programs for performing matrix-vector multiplication we see that the row-wise version needs to perform only a MPI_Allgather operation whereas the column-wise program needs to perform a MPI_Reduce and a MPI_Scatter operation.
- In general, a row-wise distribution is preferable as it leads to small communication overhead. However, many times, an application needs to compute not only
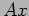 but also
but also 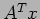 . In that case, the row-wise distribution can be used to compute
. In that case, the row-wise distribution can be used to compute 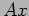 , but the computation of
, but the computation of 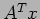 requires the column-wise distribution (a row-wise distribution of
requires the column-wise distribution (a row-wise distribution of  is a column-wise distribution of its transpose
is a column-wise distribution of its transpose 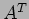 ).
).
- It is much cheaper to use the program for the column-wise distribution than to transpose the matrix and then use the row-wise program.




Next: Two-Dimensional Matrix-Vector Multiplication
Up: Introduction to Parallel Algorithms
Previous: Cannon's Matrix-Matrix Multiplication with
Contents
Cem Ozdogan
2006-12-27