Differentiation with a Computer
- The derivative of a function,
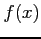 at
at  , is defined as
, is defined as
- This is called a forward-difference approximation.
- The limit could be approached from the opposite direction, giving a backward-difference approximation.
- Forward-difference approximation. A computer can calculate an approximation to the derivative, if a very small value is used for
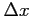 .
.
- Recalculating with smaller and smaller values of
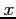 starting from an initial value.
starting from an initial value.
- What happens if the value is not small enough?
Table 1:
Forward-difference approximations for
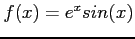 .
.
![\begin{table}\begin{center}
\includegraphics[scale=0.9,angle=0.5]{figures/5.1.ps}
\end{center}
\end{table}](img13.png) |
With MATLAB. Analytical answer to the function of Table 1.
With MATLAB. Numerical answer to the function of Table 1.
With MATLAB,
Table 2 illustrates this, showing that errors decrease about four fold when 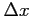 is halved (as Eq. 3 predicts) and that a more accurate value is obtained.
is halved (as Eq. 3 predicts) and that a more accurate value is obtained.
Table 2:
Central-difference approximations for
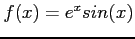 .
.
![\begin{table}\begin{center}
\includegraphics[scale=1]{figures/5.2.ps}
\end{center}
\end{table}](img32.png) |
Cem Ozdogan
2011-01-05
![]() is halved (as Eq. 3 predicts) and that a more accurate value is obtained.
is halved (as Eq. 3 predicts) and that a more accurate value is obtained.