Numerical Integration - The Trapezoidal Rule

• Given the function, 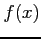$f(x)$, the antiderivative is a function 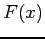$F(x)$ such that $F'(x)=f(x)$.
• The definite integral
  
  $$\int_a^b f(x)dx=F(b) - F(a)$$
  
  
  can be evaluated from the antiderivative.
• Still, there are functions that do not have an antiderivative expressible in terms of ordinary functions.

  
• Is there any way that the definite integral can be found when the antiderivative is unknown?

• We can do it numerically by using the composite trapezoidal rule

  

• The definite integral is the area between the curve of 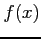$f(x)$ and the 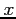$x$-axis.
• That is the principle behind all numerical integration;
• We divide the distance from $x=a$ to $x=b$ into vertical strips and add the areas of these strips.
• The strips are often made equal in widths but that is not always required.