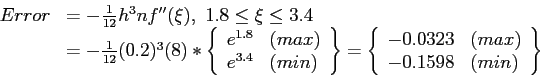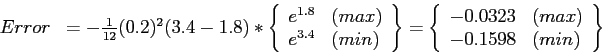The Composite Trapezoidal Rule
- We subdivide [a,b] into
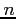 smaller intervals with
smaller intervals with 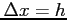 , apply the rule to each subinterval, and add.
, apply the rule to each subinterval, and add.
- This gives the composite trapezoidal rule;
- The error is not the local error
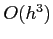 but the global error, the sum of
but the global error, the sum of 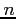 local errors;
local errors;
- In this equation, each of the
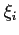 is somewhere within each subinterval.
is somewhere within each subinterval.
- If
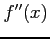 is continuous in [a, b], there is some point within [a,b] at which the sum of the
is continuous in [a, b], there is some point within [a,b] at which the sum of the 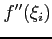 is equal to
is equal to 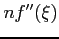 , where
, where 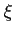 in [a, b].
in [a, b].
- We then see that, because
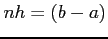 ,
,
- Example: Given the values for
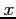 and
and 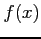 in Table3.
in Table3.
Table 3:
Example for the trapezoidal rule.
![\begin{table}\begin{center}
\includegraphics[scale=0.9]{figures/5.4.ps}
\end{center}
\end{table}](img55.png) |
- Use the trapezoidal rule to estimate the integral from
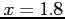 to
to 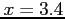 .
.
- Applying the trapezoidal rule:
- The data in Table 3 are for
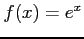 and the true value is
and the true value is
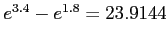 .
.
- The trapezoidal rule value is off by
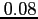 ; there are three digits of accuracy.
; there are three digits of accuracy.
- How does this compare to the estimated error?
Alternatively,
- The actual error was
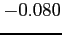 . It is reasonable since the value is in the error bounds.
. It is reasonable since the value is in the error bounds.
Thanks for attending and listening.
Cem Ozdogan
2011-01-05
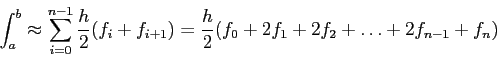
![\begin{displaymath}
\begin{array}{rl}
\int_{1.8}^{3.4}f(x)dx& \approx \frac{0.2}...
...+ 2(20.086) + 2(24.533)\\
& + 29.964] = 23.9944\\
\end{array}\end{displaymath}](img58.png)