- MATLAB Desktop.
- An illustrating example: The ladder in the mine.
- An illustrating example: The ladder in the mine. Solution with MATLAB
- Level of precision.
- Computer numbers with six bit representation.
- Upper: number line in the hypothetical system, Lower: IEEE standard.
- Left: Adding eight numbers sequentially. Right: Adding eight numbers with parallel processors.
- Testing for a change in sign of f(x) will bracket either a root or singularity.
- Plot of the function:
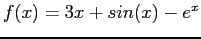
- The stopping criterion for a root-finding procedure should involve a tolerance on
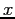 , as well as a tolerance on
, as well as a tolerance on 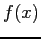 .
.
- Graphical illustration of the Secant Method.
- A pathological case for the secant method.
- Graphical illustration of the Newton's Method.
- Graphical illustration of the case that Newton's Method will not converge.
- Parabola
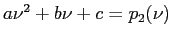
- An example of the use of Muller's method.
- Cont. An example of the use of Muller's method.
- The fixed point of
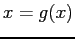 is the intersection of the line
is the intersection of the line 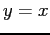 and the curve
and the curve 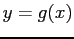 plotted against
plotted against 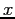 . Where A:
. Where A:
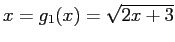 . B:
. B:
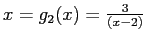 . C:
. C:
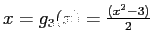 .
.
- Left: The curve on the left has a triple root at
 [the function is
[the function is 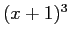 ]. The curve on the right has a double root at
]. The curve on the right has a double root at 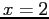 [the function is
[the function is 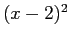 ].Right: Plot of
].Right: Plot of
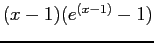 .
.
- A pair of equations.
- A curve fit function passes near the data points. An interpolating function passes exactly through the data points.
- Fitting with different degrees of the polynomial.
- Fitting with quadratic in subinterval.
- Linear spline.
- Cubic spline.
- Resistance vs Temperature graph for the Least-Squares Approximation.
- Minimizing the deviations by making the sum a minimum.
- Figure for the data to illustrate curve fitting.
- The graph of
 vs
vs 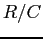 .
.
- plot(x,Y,'o',x,y,'-').
- plot(x,Y,'o',x,f,'-',x,y,'+').
- Plot of the first four polynomials of the Chebyshev polynomials.
- Comparison of the error of Chebyshev series for
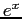 with the error of Maclaurin series.
with the error of Maclaurin series.
- plot(x,errorchebyshev,'o',x,errormaclaurin,'-').
- Plot of a periodic function of period P.
- Left: Plot of
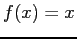 , periodic of period
, periodic of period 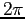 ,Right: Plot of the Fourier series expansion for
,Right: Plot of the Fourier series expansion for 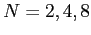 .
.
- Plot of Fourier series for
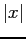 for
for 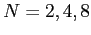 .
.
- Plot of Fourier series for
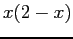 for
for 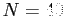 .
.
- A function,
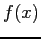 , of interest on [0,3].
, of interest on [0,3].
- Left: Plot of a function reflected about the y-axis, an even function,Right: Plot of a function reflected about the origin, an odd function.
- Left: Plot of the function reflected about the y-axis, Right: Plot of the function reflected about the origin.
- The trapezoidal rule.
Cem Ozdogan
2011-12-27